此内容为信号与系统课程课内大作业
学会用MATLAB画连续离散系统零极点图; 学会用MATLAB分析连续、离散系统的频率特性; 画出系统的幅频特性曲线 画出系统的相频特性曲线 sys = tf(num, den) : 传递函数, num 是系统分子向量, den 是系统分母向量求系统零点极点图: 调用函数 pzmap(sys) 画出系统的零点极点图求系统的幅频特性,并画出系统的幅频特性曲线和相频特性曲线: 调用函数h = freqs(num, den, w) 根据系数向量计算返回模拟滤波器的复频域响应。freqs 计算在复平面虚轴上的频率响应h,角频率w确定了输入的实向量,因此必须包含至少一个频率点。[z, p, k] = tf2zp(B, A) B 是系统分子向量,A 是系统分母向量, z, p, k 分别是零点、极点和增益求系统零点极点图: 调用函数 zplane(B, A) 画出系统的零点极点图求系统的幅频特性,并画出系统的幅频特性曲线和相频特性曲线: 调用函数h = freqz(num, den, w) 根据系数向量计算返回模拟滤波器的复频域响应。freqs 计算在复平面虚轴上的频率响应h,角频率w确定了输入的实向量,因此必须包含至少一个频率点。分别求下面两个函数的零点极点图、幅频特性曲线和相频特性曲线
连续系统:H ( s ) = 0.2 s 2 + 0.3 s + 1 s 2 + 0.4 + 1 H(s) = \cfrac{0.2s^2 + 0.3s+1}{s^2 + 0.4+1} H ( s ) = s 2 + 0.4 + 1 0.2 s 2 + 0.3 s + 1
离散系统:H ( z ) = z − 0.5 z H(z) = \cfrac{z-0.5}{z} H ( z ) = z z − 0.5
实验源代码:
连续系统:
clc;
clear;
a = [ 1 0.4 1 ] ;
b = [ 0.2 0.3 1 ] ;
w = logspace ( - 1 , 1 ) ;
sys = tf ( b, a) ;
figure ( 1 ) ; pzmap ( sys) ;
figure ( 2 ) ; freqs ( b, a, w) ;
离散系统:
clc;
clear;
a = [ 1 , 0 ] ;
b = [ 1 , 0.5 ] ;
figure ( 1 ) ; zplane ( b, a) ;
figure ( 2 ) ; freqz ( b, a, 400 ) ;
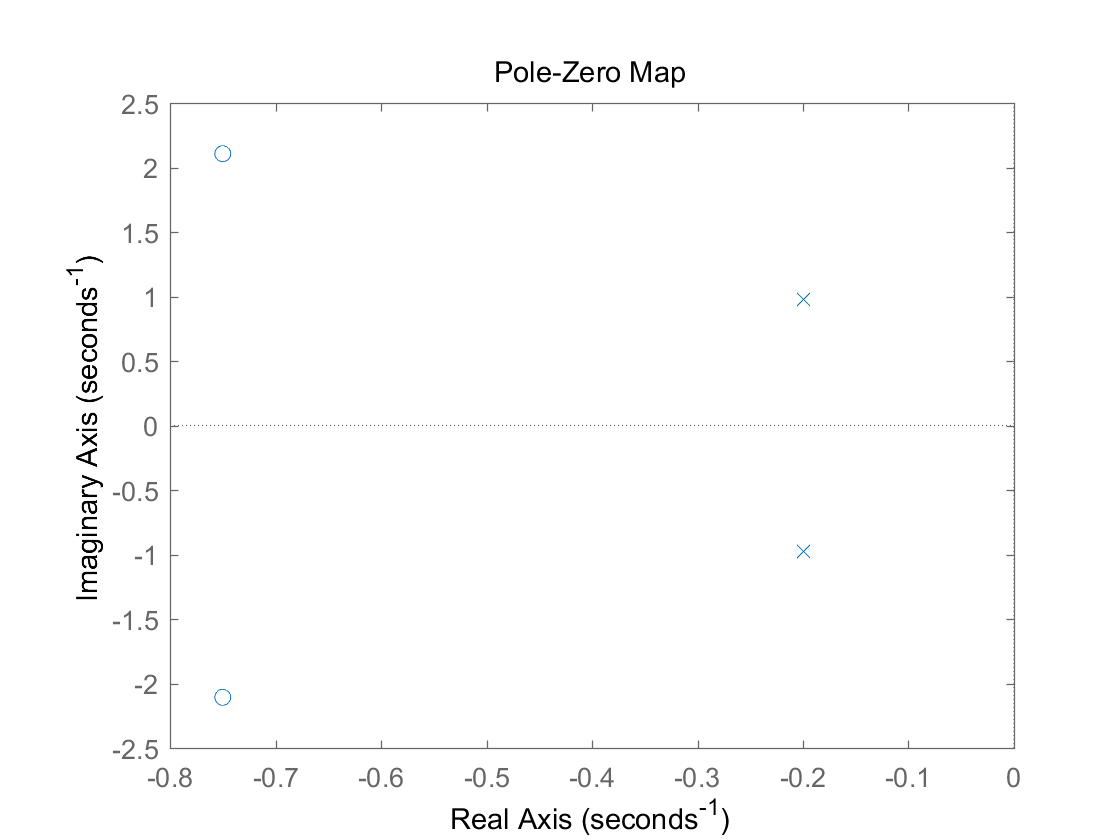
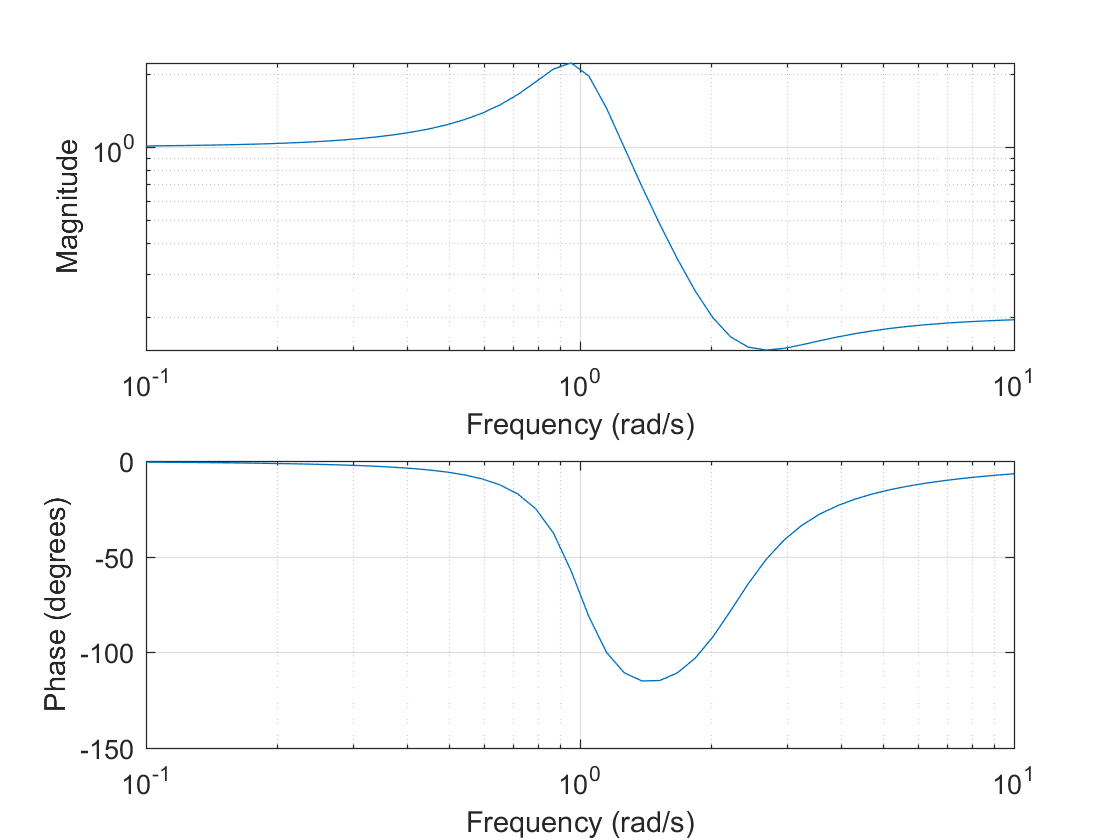
(1) 连续系统: H ( s ) = 0.2 s 2 + 0.3 s + 1 s 2 + 0.4 + 1 H(s) = \cfrac{0.2s^2 + 0.3s+1}{s^2 + 0.4+1} H ( s ) = s 2 + 0.4 + 1 0.2 s 2 + 0.3 s + 1
零点极点图:
幅频、相频特性曲线:
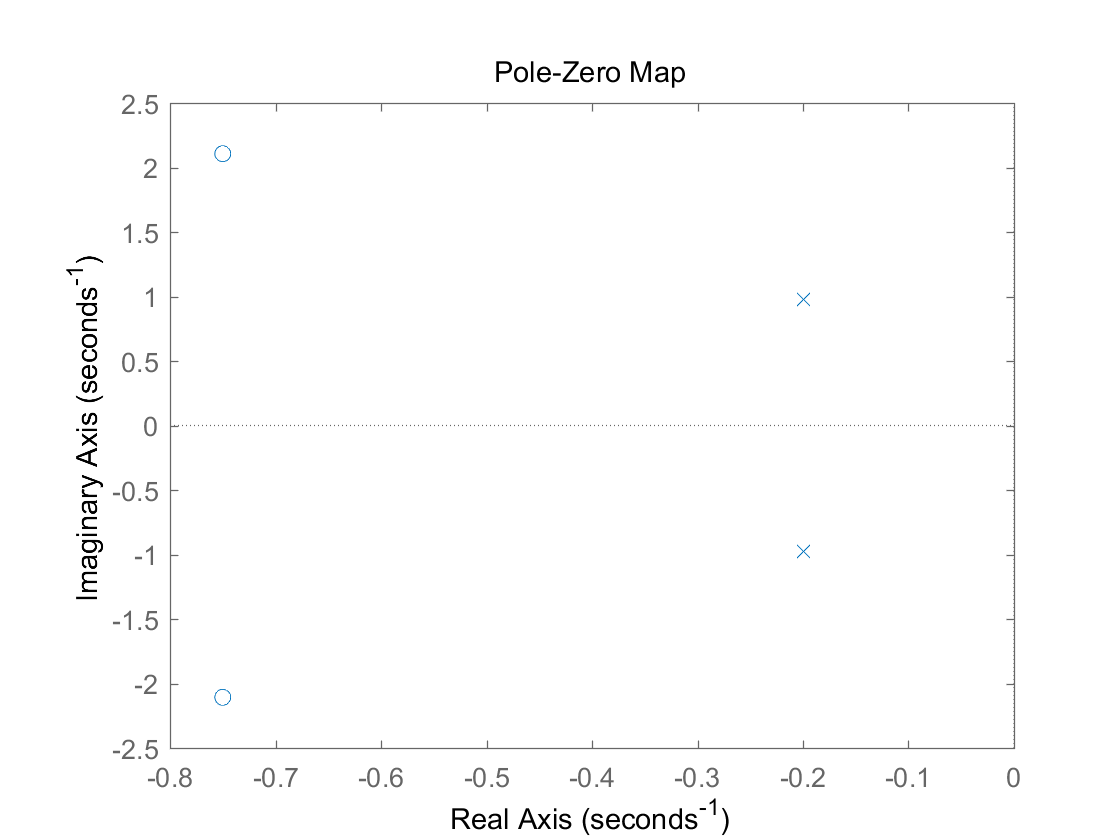
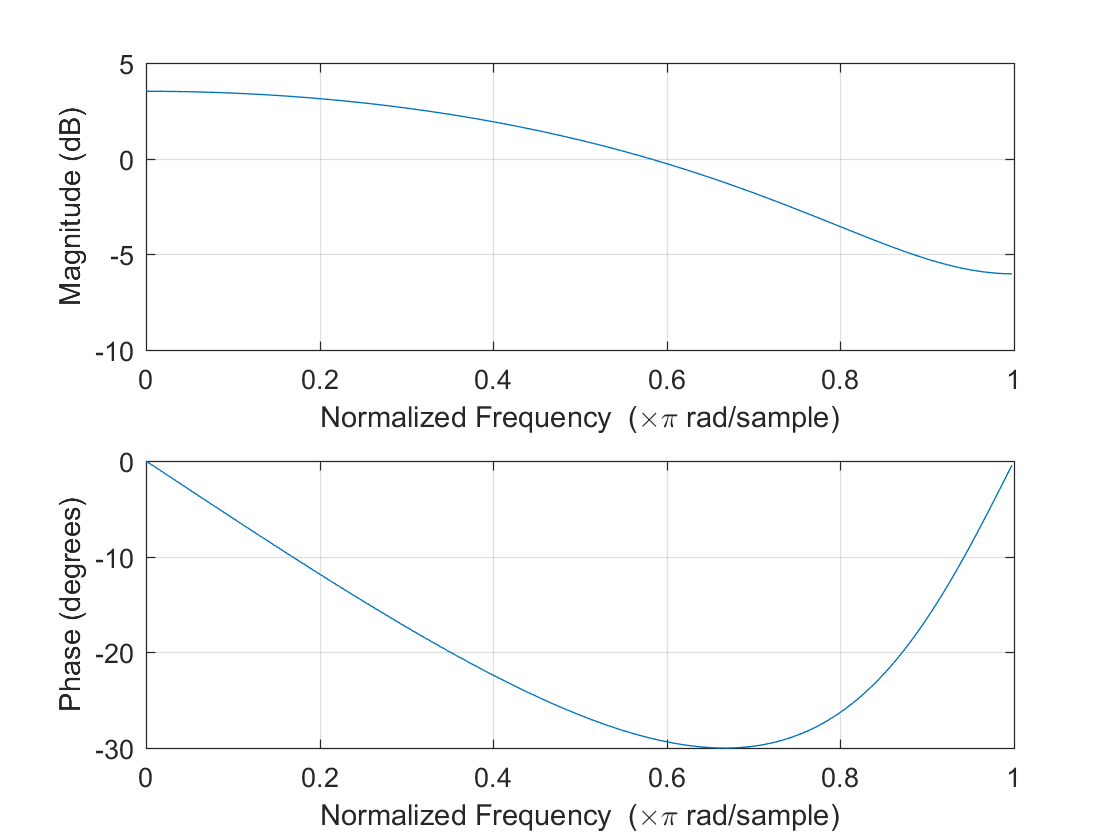
(2) 离散系统: H ( z ) = z − 0.5 z H(z) = \cfrac{z-0.5}{z} H ( z ) = z z − 0.5
零点极点图:
幅频、相频特性曲线:
统一判定公式:
判定线性系统条件:
T [ a x 1 ( t ) + b x 2 ( t ) ] = ? T [ a x 1 ( t ) ] + T [ b x 2 ( t ) ] T[ax_1(t)+bx_2(t)] \overset{?}{=} T[ax_1(t)] + T[bx_2(t)] T [ a x 1 ( t ) + b x 2 ( t )] = ? T [ a x 1 ( t )] + T [ b x 2 ( t )]
判定时不变系统条件:
T [ x ( t − t 0 ) ] = ? y ( t − t 0 ) T[x(t-t_0)] \overset{?}{=} y(t-t_0) T [ x ( t − t 0 )] = ? y ( t − t 0 )
例:判定 $y(t) = x(t)^2 $是否为线性系统
解:
根据线性系统的判定条件:
T [ a x 1 ( t ) + b x 2 ( t ) ] = [ a x 1 ( t ) + b x 2 ( t ) ] 2 T[ax_1(t) + bx_2(t)] = [ax_1(t)+bx_2(t)]^2 T [ a x 1 ( t ) + b x 2 ( t )] = [ a x 1 ( t ) + b x 2 ( t ) ] 2
即:将原式中的 x ( t ) x(t) x ( t ) a x 1 ( t ) + b x 2 ( t ) ax_1(t) + bx_2(t) a x 1 ( t ) + b x 2 ( t )
T [ a x 1 ( t ) ] + T [ b x 2 ( t ) ] = [ a x 1 ( t ) ] 2 + [ b x 2 ( t ) ] 2 T[ax_1(t)] + T[bx_2(t)] = [ax_1(t)]^2+[bx_2(t)]^2 T [ a x 1 ( t )] + T [ b x 2 ( t )] = [ a x 1 ( t ) ] 2 + [ b x 2 ( t ) ] 2
二者并不相等,因此此系统为非线性系统。
例:判定 y ( t ) = c o s ( w t ) x ( t ) y(t) = cos(wt)x(t) y ( t ) = cos ( wt ) x ( t )
解:
根据时不变系统的判定条件:
T [ x ( t − t 0 ) ] = c o s ( w t ) x ( t − t 0 ) y ( t − t 0 ) = c o s [ w ( t − t 0 ) ] x ( t − t 0 ) T[x(t-t_0)] = cos(wt)x(t-t_0)\\ y(t-t_0) = cos[w(t-t_0)]x(t-t_0) T [ x ( t − t 0 )] = cos ( wt ) x ( t − t 0 ) y ( t − t 0 ) = cos [ w ( t − t 0 )] x ( t − t 0 )
二者并不相等,因此此系统为时变系统。
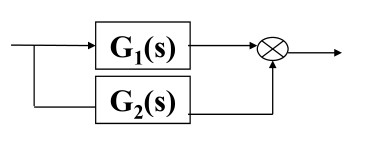
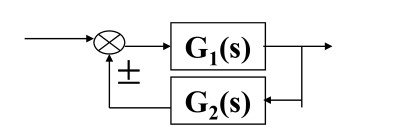
三种基本变换:
串联 img ϕ ( s ) = G 1 ( s ) G 2 ( s ) \phi(s) = G_1(s)G_2(s) ϕ ( s ) = G 1 ( s ) G 2 ( s )
并联 img ϕ ( s ) = G 1 ( s ) + G 2 ( s ) \phi(s) = G_1(s)+G_2(s) ϕ ( s ) = G 1 ( s ) + G 2 ( s )
反馈 img ϕ ( s ) = G 1 ( s ) 1 ± G 2 ( s ) \phi(s) = \cfrac{G_1(s)}{1\pm G_2(s)} ϕ ( s ) = 1 ± G 2 ( s ) G 1 ( s )
梅森公式:
ϕ ( s ) = ∑ P k Δ k Δ \phi(s)=\frac{\sum P_{k} \Delta_{k}}{\Delta} ϕ ( s ) = Δ ∑ P k Δ k
Δ = 1 − ∑ L i + ∑ L i L j − ∑ L i L j L k + ⋯ \Delta=1-\sum L_{i}+\sum L_{i} L_{j}-\sum L_{i} L_{j} L_{k}+\cdots Δ = 1 − ∑ L i + ∑ L i L j − ∑ L i L j L k + ⋯
∑ L i \sum L_{i} ∑ L i ∑ L i L j \sum L_{i} L_{j} ∑ L i L j ∑ L i L j L k \sum L_{i} L_{j} L_{k} ∑ L i L j L k P k P_{k} P k K K K Δ k \Delta_{k} Δ k Δ \Delta Δ K K K Δ \Delta Δ 例: 利用梅森公式对下列流程图进行化简:
在这里插入图片描述 系统回路:
L 1 = − G 1 ( s ) G 2 ( s ) H 1 ( s ) L 2 = − G 2 ( s ) G 3 ( s ) H 2 ( s ) L 3 = − G 1 ( s ) G 2 ( s ) G 3 ( s ) L 4 = − G 1 ( s ) G 4 ( s ) L 5 = − G 4 ( s ) H 2 ( s ) L_1 = -G_1(s)G_2(s)H_1(s)\\ L_2 = -G_2(s)G_3(s)H_2(s)\\ L_3 = -G_1(s)G_2(s)G_3(s)\\ L_4 = -G_1(s)G_4(s)\\ L_5=-G_4(s)H_2(s) L 1 = − G 1 ( s ) G 2 ( s ) H 1 ( s ) L 2 = − G 2 ( s ) G 3 ( s ) H 2 ( s ) L 3 = − G 1 ( s ) G 2 ( s ) G 3 ( s ) L 4 = − G 1 ( s ) G 4 ( s ) L 5 = − G 4 ( s ) H 2 ( s )
无相互不接触的回路,即:
∑ L i L j = 0 \sum L_iL_j=0 ∑ L i L j = 0
则,特征式为:
Δ = 1 − ∑ L i = 1 + G 1 ( s ) G 2 ( s ) H 1 ( s ) + G 2 ( s ) G 3 ( s ) H 2 ( s ) + G 1 ( s ) G 2 ( s ) G 3 ( s ) + G 1 ( s ) G 4 ( s ) + G 4 ( s ) H 2 ( s ) \Delta = 1-\sum L_i\\ =1+G_1(s)G_2(s)H_1(s)+G_2(s)G_3(s)H_2(s)+G_1(s)G_2(s)G_3(s)+G_1(s)G_4(s)+G_4(s)H_2(s) Δ = 1 − ∑ L i = 1 + G 1 ( s ) G 2 ( s ) H 1 ( s ) + G 2 ( s ) G 3 ( s ) H 2 ( s ) + G 1 ( s ) G 2 ( s ) G 3 ( s ) + G 1 ( s ) G 4 ( s ) + G 4 ( s ) H 2 ( s )
前向通路:
P 1 ( s ) = G 1 ( s ) G 2 ( s ) G 3 ( s ) P 2 = G 1 ( s ) G 4 ( s ) P_1(s) = G_1(s)G_2(s)G_3(s) \\P_2 = G_1(s)G_4(s) P 1 ( s ) = G 1 ( s ) G 2 ( s ) G 3 ( s ) P 2 = G 1 ( s ) G 4 ( s )
对应的余子式为:
Δ 1 = 1 Δ 2 = 1 \Delta_1 =1\\ \Delta_2 = 1 Δ 1 = 1 Δ 2 = 1
则对应的传递函数是:
ϕ ( s ) = ∑ P k Δ k Δ = P 1 + P 2 Δ = G 1 ( s ) G 2 ( s ) G 3 ( s ) + G 1 ( s ) G 4 ( s ) 1 + G 1 ( s ) G 2 ( s ) H 1 ( s ) + G 2 ( s ) G 3 ( s ) H 2 ( s ) + G 1 ( s ) G 2 ( s ) G 3 ( s ) + G 1 ( s ) G 4 ( s ) + G 4 ( s ) H 2 ( s ) \phi(s)=\frac{\sum P_{k} \Delta_{k}}{\Delta} = \cfrac{P_1+P_2}{\Delta}\\ =\cfrac{G_1(s)G_2(s)G_3(s)+G_1(s)G_4(s)}{1+G_1(s)G_2(s)H_1(s)+G_2(s)G_3(s)H_2(s)+G_1(s)G_2(s)G_3(s)+G_1(s)G_4(s)+G_4(s)H_2(s)} ϕ ( s ) = Δ ∑ P k Δ k = Δ P 1 + P 2 = 1 + G 1 ( s ) G 2 ( s ) H 1 ( s ) + G 2 ( s ) G 3 ( s ) H 2 ( s ) + G 1 ( s ) G 2 ( s ) G 3 ( s ) + G 1 ( s ) G 4 ( s ) + G 4 ( s ) H 2 ( s ) G 1 ( s ) G 2 ( s ) G 3 ( s ) + G 1 ( s ) G 4 ( s )
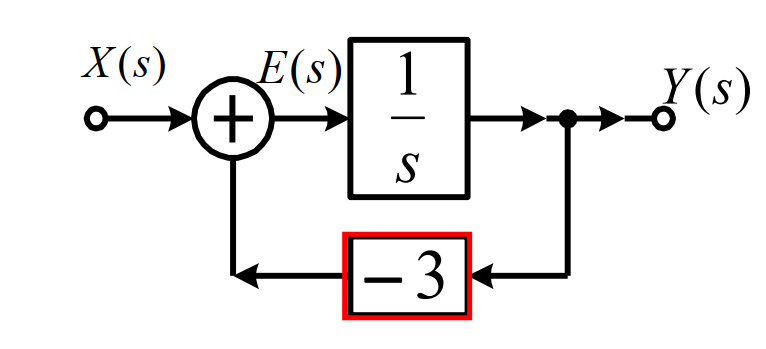
从例题感悟绘制方法
H ( s ) = 1 s + 3 = Y ( s ) X ( s ) H(s)=\frac{1}{s+3}=\frac{Y(s)}{X(s)} H ( s ) = s + 3 1 = X ( s ) Y ( s )
Let
E ( s ) = s Y ( s ) E(s)=s Y(s) E ( s ) = s Y ( s )
Then,
1 s E ( s ) = Y ( s ) E ( s ) = X ( s ) − 3 Y ( s ) \begin{gathered} \cfrac{1}{s} E(s)=Y(s) \\ E(s)=X(s)-3 Y(s) \end{gathered} s 1 E ( s ) = Y ( s ) E ( s ) = X ( s ) − 3 Y ( s )
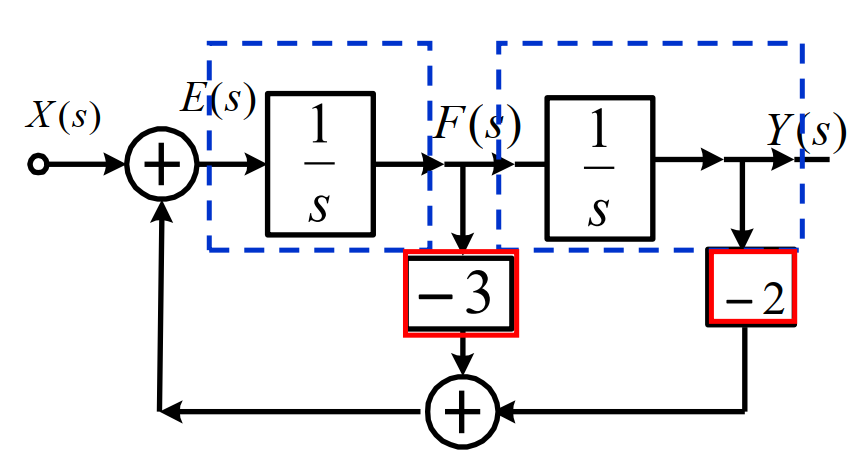
H ( s ) = 1 s 2 + 3 s + 2 = Y ( s ) X ( s ) H(s)=\cfrac{1}{s^{2}+3 s+2}=\cfrac{Y(s)}{X(s)} H ( s ) = s 2 + 3 s + 2 1 = X ( s ) Y ( s )
(1) Direct-form Let
F ( s ) = s Y ( s ) E ( s ) = s F ( s ) = s 2 Y ( s ) F(s)=s Y(s) \\ E(s)=s F(s)=s^{2} Y(s) F ( s ) = s Y ( s ) E ( s ) = s F ( s ) = s 2 Y ( s )
Then,
E ( s ) = X ( s ) − 3 F ( s ) − 2 Y ( s ) E(s)=X(s)-3 F(s)-2 Y(s) E ( s ) = X ( s ) − 3 F ( s ) − 2 Y ( s )
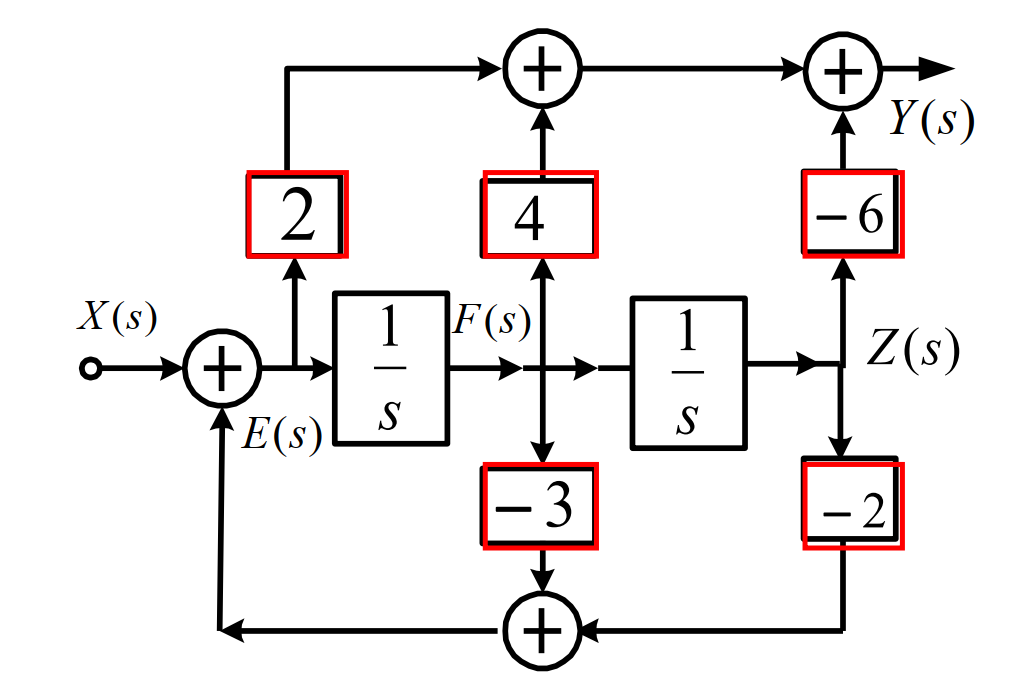
H ( s ) = 2 s 2 + 4 s − 6 s 2 + 3 s + 2 H ( s ) = ( 1 s 2 + 3 s + 2 ) ( 2 s 2 + 4 s − 6 ) = Y ( s ) X ( s ) Let Z ( s ) = 1 s 2 + 3 s + 2 X ( s ) ( 2 s 2 + 4 s − 6 ) Z ( s ) = Y ( s ) F ( s ) = s Z ( s ) E ( s ) = s F ( s ) = s 2 Z ( s ) Y ( s ) = ( 2 s 2 + 4 s − 6 ) Z ( s ) = 2 E ( s ) + 4 F ( s ) − 6 Z ( s ) H(s)=\cfrac{2 s^{2}+4 s-6}{s^{2}+3 s+2} \\ H(s)=\left(\cfrac{1}{s^{2}+3 s+2}\right)\left(2 s^{2}+4 s-6\right)=\frac{Y(s)}{X(s)} \\ \text { Let } Z(s)=\cfrac{1}{s^{2}+3 s+2} X(s) \\ \left(2 s^{2}+4 s-6\right) Z(s)=Y(s) \\ F(s)=s Z(s) E(s)=s F(s)=s^{2} Z(s) \\ Y(s)=\left(2 s^{2}+4 s-6\right) Z(s) \\ =2 E(s)+4 F(s)-6 Z(s) H ( s ) = s 2 + 3 s + 2 2 s 2 + 4 s − 6 H ( s ) = ( s 2 + 3 s + 2 1 ) ( 2 s 2 + 4 s − 6 ) = X ( s ) Y ( s ) Let Z ( s ) = s 2 + 3 s + 2 1 X ( s ) ( 2 s 2 + 4 s − 6 ) Z ( s ) = Y ( s ) F ( s ) = s Z ( s ) E ( s ) = s F ( s ) = s 2 Z ( s ) Y ( s ) = ( 2 s 2 + 4 s − 6 ) Z ( s ) = 2 E ( s ) + 4 F ( s ) − 6 Z ( s )