跳至主要內容

数据结构 —— 线性表、栈、队列、串

CK...大约 17 分钟建模算法数据结构算法C语言

数据结构 —— 线性表、栈、队列、串

当我开始这篇博客的书写时，我将知道，这是一个艰难而且繁杂的过程。一向追求实际作用的我，在学习数据分析、网络爬虫乃至自动化和前端UI等更能看得见摸得着的东西时，更能保持我的积极性和专注力。而以数据结构为代表的算法，始终无法让我静下心来，慢慢研究。我知道，算法的背后是数学，而要想让自己的编程技术上一个台阶，学习算法是必不可少的。这篇博客以程杰老师的《大话数据结构》为依托，写下我对相关数据结构的总结和学习笔记。希望对您和我都有十足的帮助。

CK出品，必属精品！

数据结构概述

程序设计 = 数据结构 + 算法

基本概念和术语

数据： 描述客观事物的符号，是计算机中可以操作的对象，是能被计算机识别，并输入给计算机处理的符号集合。

数据不仅仅包括、等数值类型，还包括以及、、等非数值类型。

数据元素： 是组成数据的、有一定意义的基本单位，再计算机中通常作为整体处理。也被称为记录。

数据项： 一个数据元素可以由若干个数据项组成。数据项是数据不可分割的最小单位。

数据对象： 是性质相同的数据元素的集合，是数据的子集。

数据结构： 是相互之间存在一种或多种特定关系的数据元素的集合。

抽象数据类型（Absrtract Data Type）： 是指一个数学模型及定义

ADT 抽象数据结构
Data 
	数据元素之间的逻辑关系定义
Operation
	操作1
		初始条件
		操作结果描述
	操作2
		...
	操作3
		...
endADT

线性表

线性表的抽象数据类型定义如下：

ADT 线性表（List）
Data
	线性表的数据对象集合是{a, b, c, ...}，每个元素的类型均为 DataType。其中，除第一个元素外，每一个元素有且只有一个直接前驱元素，除了最后一个元素外，每一个元素有且只有一个直接后驱元素。数据元素之间的关系是一对一的。
Operation
	InitList(*L): 初始化操作，建立一个线性表L。
	ListEmpty(L): 若线性表为空，返回 true，否则返回 false。
	ClearList(*L): 将线性表清空。
	GetElem(L, i, *e): 将线性表L中的第 i 个元素值返回给 e。
	LocateElem(*L, e): 查找线性表中与 e 相同的元素,返回其序号,若不存在则返回 0.
	Listinsert(*L, i, e): 将 e 元素插入到 L 中的第 i 个位置.
	ListDelete(*L, i, *e): 删除线性表 L 中的第 i 个位置元素, 并将其值返回给 e.
	ListLength(L): 返回 L 中的元素个数.
endADT

线性表的顺序存储结构 (SqList)

在算法的代码实现之前，首先声明展示这些定义和重命名，能够让我们的代码的可读性进一步提高：

#define MAXSIZE 20
#define OK 1
#define ERROR 0
#define TRUE 1
#define False 0

typedef int ElemType;
typedef int Status;

在 C语言中，存储线性表的顺序存储结构是数组，所以可以定义下面的顺序存储结构代码：

typedef int ElemType;
typedef struct {
    ElemType data[MAXSIZE];
    int length;
}SqLsit;

获取元素操作

// 获得数据元素
Status GetElem(SqList L, int pos, ElemType* e){
    // 如果获取元素的位置小于 1 或者大于线性表长度，则返回错误
    if(pos < 1 || pos > L.length){
        return ERROR;
    }else{
        // 将第 pos - 1个元素赋给 e
        *e = L.data[pos - 1];
        return OK;
    }
}

插入元素操作

// 插入元素操作
Status ListInsert(SqList * L, int pos, ElemType e){
    // 如果插入元素的位置小于 1 或者大于线性表的长度 或者线性表的长度为 MAXSIZE，则返回错误
    if(pos < 1 || pos > L->length+1 || L->length == MAXSIZE){
        return ERROR;
    }
    // 若插入元素不在表尾
    else if(pos <= L->length){
        // 将线性表中从 length-1 到 pos-1 全部向后移动一位
        for (int i = L->length-1; i >= pos-1 ; --i) {
            L->data[i+1] = L->data[i];
        }
    }
    // 将元素 e 赋给线性表中的 pos-1
    L->data[pos-1] = e;
    L->length ++;
    return OK;
}

删除元素操作

// 删除元素操作
Status ListDelete(SqList * L, int pos, ElemType* e){
    // 如何删除元素的位置小于 1 或者大于线性表长度，返回错误
    if(pos < 1 || pos > L->length){
        return ERROR;
    }
    // 将第 pos-1 个元素赋值给 e
    *e = L->data[pos-1];
    // 如果不是删除最后一个元素
    if(pos < L->length){
        // 将第 pos 到第 length-1 元素向前移动一位
        for (int i = pos; i < L->length; ++i) {
            L->data[i-1] = L->data[i];
        }
    }
    L->length --;
    return OK;
}

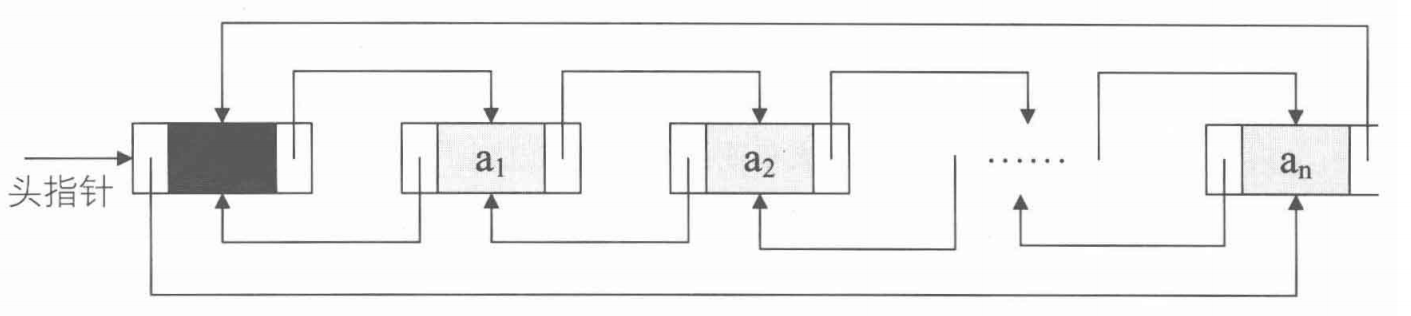
n个结点链结成一个链表，即为线性表的链式存储结构，因为链表的每个结点中只包含一个指针域，所以叫做单链表。

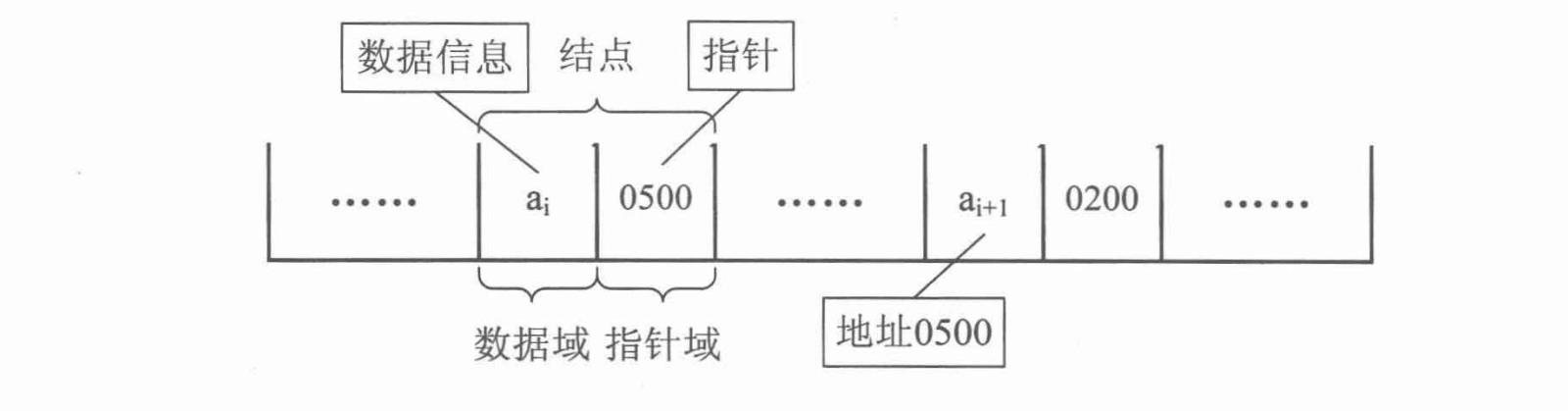
单链表的第一个结点的存储位置叫做头指针，那么整个链表的存取就必须从头指针开始进行了。最后一个链表的结点指针域为空。

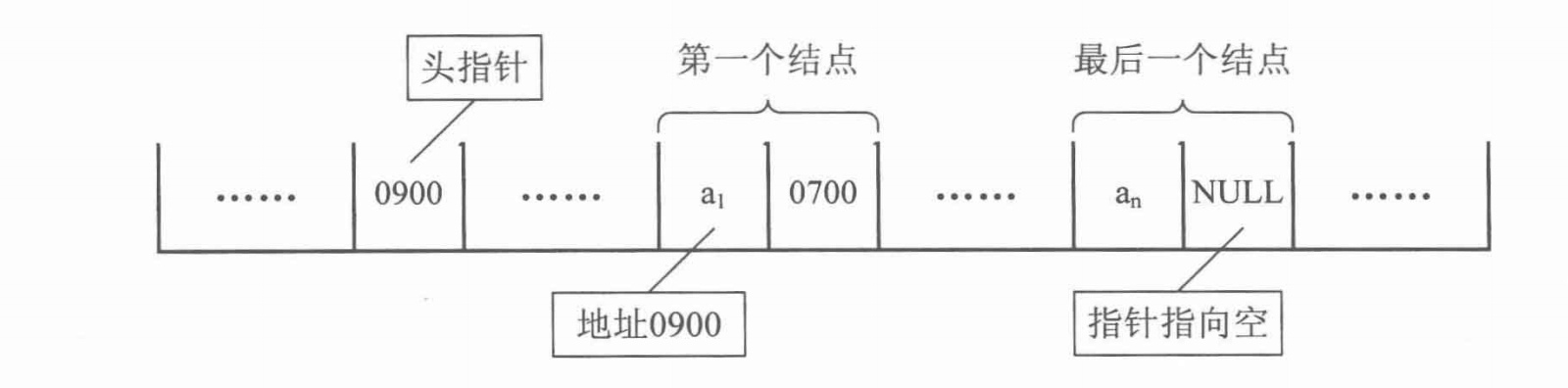
Screenshot_20220107_174033_cn.wps.moffice_eng_edit_34928506304486

有时，我们为了更加方便地对链表进行操作，会在单链表的第一个结点前附设一个结点，称为头结点。头结点的数据域可以不存储任何信息，或者有时也可以存储如线性表的长度等附加信息。

头指针和头结点的异同：

头指针：

  • 是指向链表第一个结点的指针，若链表有头结点，头指针指向头结点。
  • 头指针具有标识作用，所以常用头指针冠以链表的名字
  • 无论链表是否为空，头指针均不为空。头指针是链表的必要元素

头结点：

  • 头结点是为了操作的统一和方便而设立的，放在第一元素的结点之前，其数据域一般无意义（也可存放链表的长度）
  • 有了头结点，对在第一元素结点前插入结点和删除第一结点，其操作与其它结点的操作就统一了
  • 头结点不一定是链表必须要素

综上，带有头结点的单链表可以用下图表示：

image-20220107180450886

而空的单链表可以用下图所示：

image-20220107180521384
typedef struct Node{
    ElemType data;
    struct Node* next;
}Node;

读取元素操作

Status GetElem(LinkList L, int pos, ElemType* e){
    // 定义计数器和遍历指针
    int j = 1;
    LinkList p = L -> next;
    // 当 p 不为空并且 j < i 时工作指针后移
    while(p && j < i){
        p = p->next;
        j++;
    }
    // 如果 p 为空，则返回ERROR
    if(!p)
    	return ERROR;

    *e = p->data;
     return OK;
}

插入元素操作

image-20220108114106336

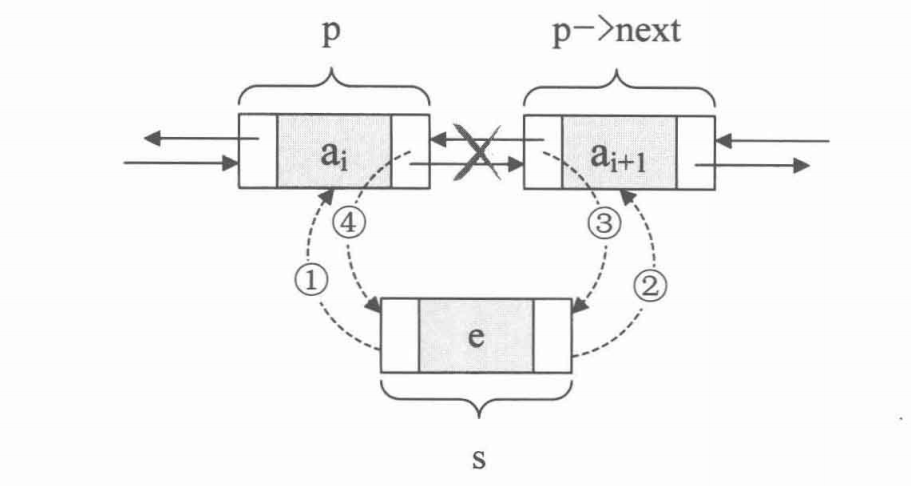
若想将 s 结点插入到 p 结点和 p->next 结点之间，只需要将 p->next 和 s->next 做一点改变即可。即做出如下操作：

s->next = p->next;
p->next = s;

注意：这两句代码不可交换位置

对于单链表的表头和表尾的特殊情况，操作是相同的：

image-20220108114521034
// 单链表元素的插入
Status ListInsert(LinkList *L, int pos, ElemType e){
    // 定义计数器和工作指针
    int j = 1;
    LinkList p = *HL;
    // 遍历，寻找目标位置的前一个结点
    while(p && j < pos){
        p = p->next;
        j++;
    }
    // 如果 p 不存在，返回 ERROR
    if (!p)
        return ERROR;
    LinkList s = (LinkList) malloc(sizeof(Node));
    s->data = e;
    s->next = p->data;
    p->next = s;
    return OK;
}

删除元素操作

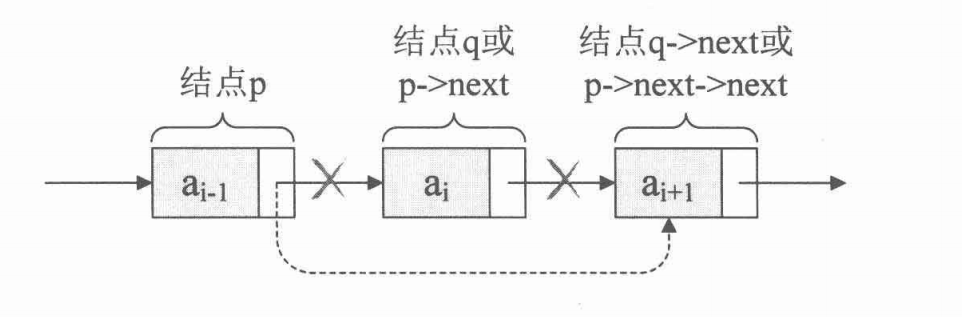
image-20220108121244436

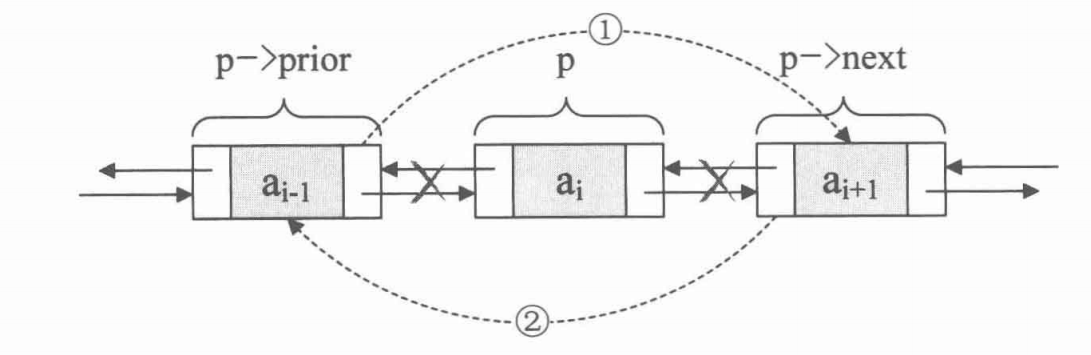
若想将 q 结点删除，只需要将 p->next 做一点改变即可。即做出如下操作：

q = p->next;
p->next = q->next;
free(q);

注意：这两句代码不可交换位置

Status ListDelete(LinkList * L, int pos, ElemType* e){
    // 定义计数器和工作指针
    int j = 1;
    LinkList p = *L;
    // 遍历到目标位置的前一个结点
    while (p && j < pos){
        p = p->next;
        j++;
    }
    if(!p){
        return ERROR;
    }
    // 删除p的下一个元素
    LinkList q = p->next;
    p->next = q->next;
    *e = q->data;
    free(q);
    return OK;
}

单链表的整表创建

整表创建的算法思路：

  1. 声明一结点 p 和计数器变量 i；
  2. 初始化一空链表；
  3. 让 L 的头结点指针指向 NULL，即建立一个带头结点的空链表；
  4. 循环：

头插法：

// 头插法创建一个空列表
void CreateListHead(LinkList *L, int n) {
    LinkList p;
    srand(time(0));
    // 初始化头结点
    *L = (LinkList) malloc(sizeof(Node));
    (*L)->next = NULL;
    for (int i = 0; i < n; ++i) {
        // 生成新结点
        p = (LinkList) malloc(sizeof (Node));
        p->data = rand()%100 +1;
        // 插入到头结点后
        p->next = (*L)->next;
        (*L)->next = p;
    }
}

尾插法：

// 尾插法创建一个空列表
void CreateListTail(LinkList *L, int n){
    LinkList p,r;
    srand(time(0));
    // 初始化头结点
    *L = (LinkList)malloc(sizeof(Node));
    (*L)->next = NULL;
    // r 为指向尾部的结点
    r = *L;
    for (int i = 0; i < n; ++i) {
        // 生成新结点
        p = (LinkList) malloc(sizeof (Node));
        p->data = rand()%100 +1;
        r->next = p;
        r = p;
    }
    r -> next = NULL;
}

单链表的整表删除

Status ClearList(LinkList * L){
    LinkList p,q;
    // p指向第一个结点
    p = (*L) -> next;
    while (p)
    {
        q = p->next;
        free(p);
        p = q;
    }
    (*L)->next = NULL;
    return OK;
}

线性表的其他存储结构

静态链表

用数组描述的链表叫做静态链表

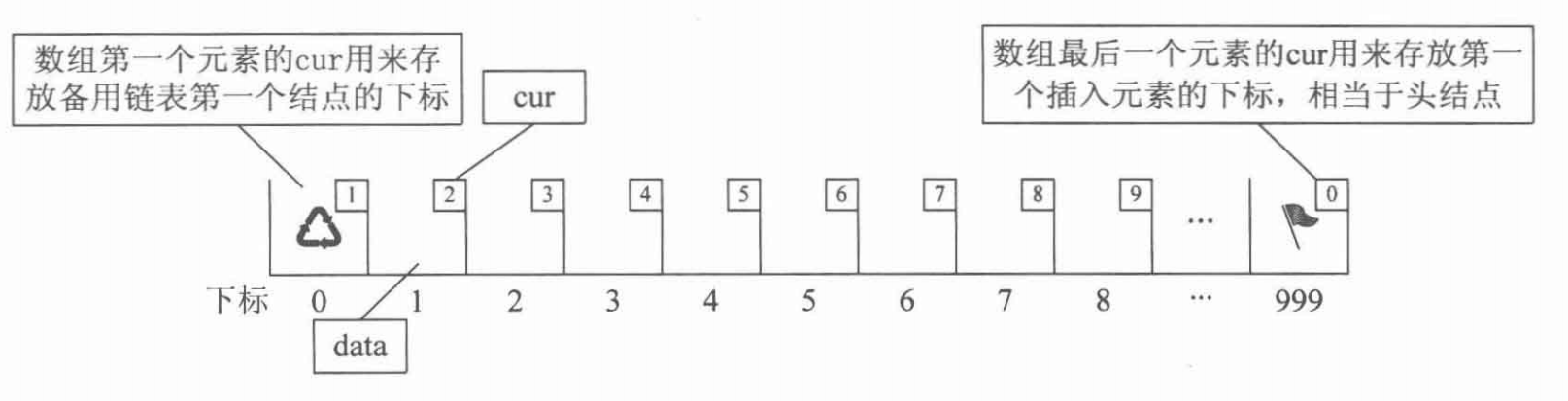
image-20220108142916662
#define MAXSIZE 1000
typedef int ElemType;
typedef struct
{
    ElemType data;
    int cur; // 游标（Cursor）
}Component, StaticLinkList[MAXSIZE];

双向链表

**双向链表( double linked list)是在单链表的每个结点中，再设置一个指向其前驱结点的指针域。**所以在双向链表中的结点都有两个指针域，一个指向直接后继，另一个指向直接前驱。

image-20220108145138863
typedef struct DulNode{
    ElemType data;
    struct DulNode* prior;
    struct DulNode* next;
}DulNode, *DuLinkList;

双向链表在插入和删除的过程中，需要额外指定一个指针变量

插入操作：

image-20220108145450166
s->perior = p;
s->next = p->next;
p->next->perior = s;
p->next = s;

s插入顺序的关键在于先解决 s 在解决 s->next的前驱，最后解决 s->perior 的后继。

删除操作：

image-20220108145739771
p->prior->next = p->next;
p->next->prior = p->prior;
free(p);

循环列表

image-20220108150409510

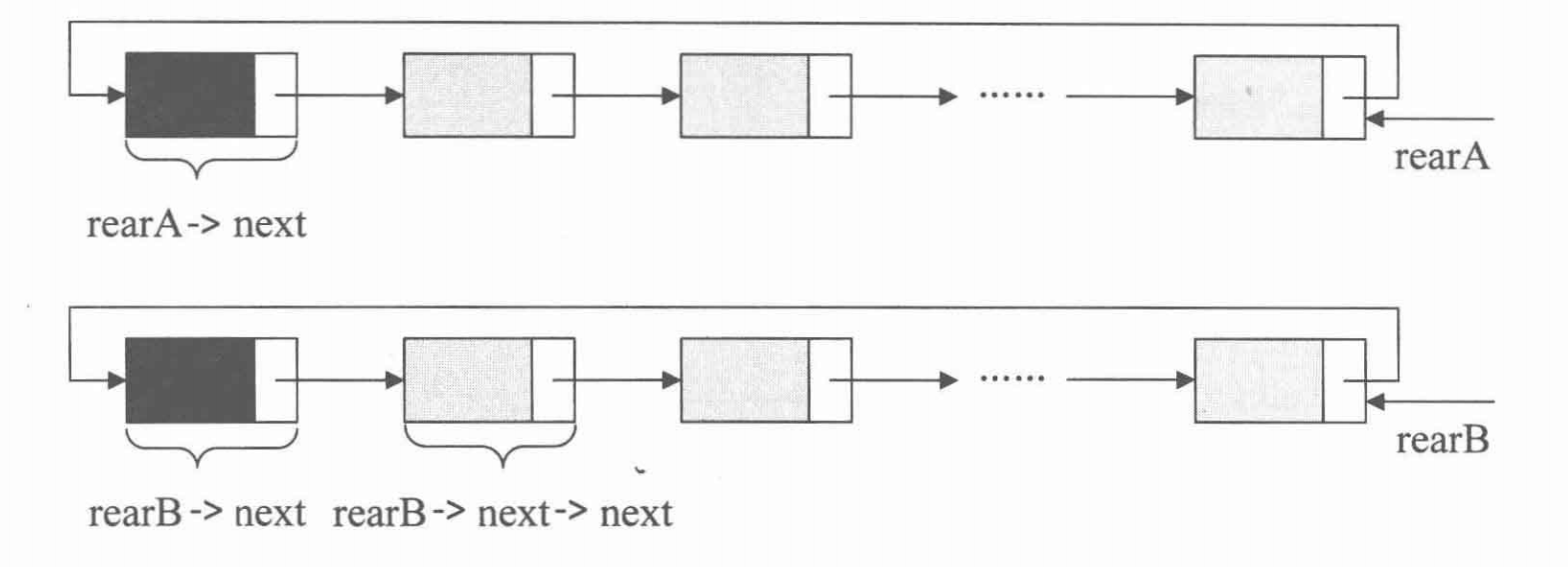
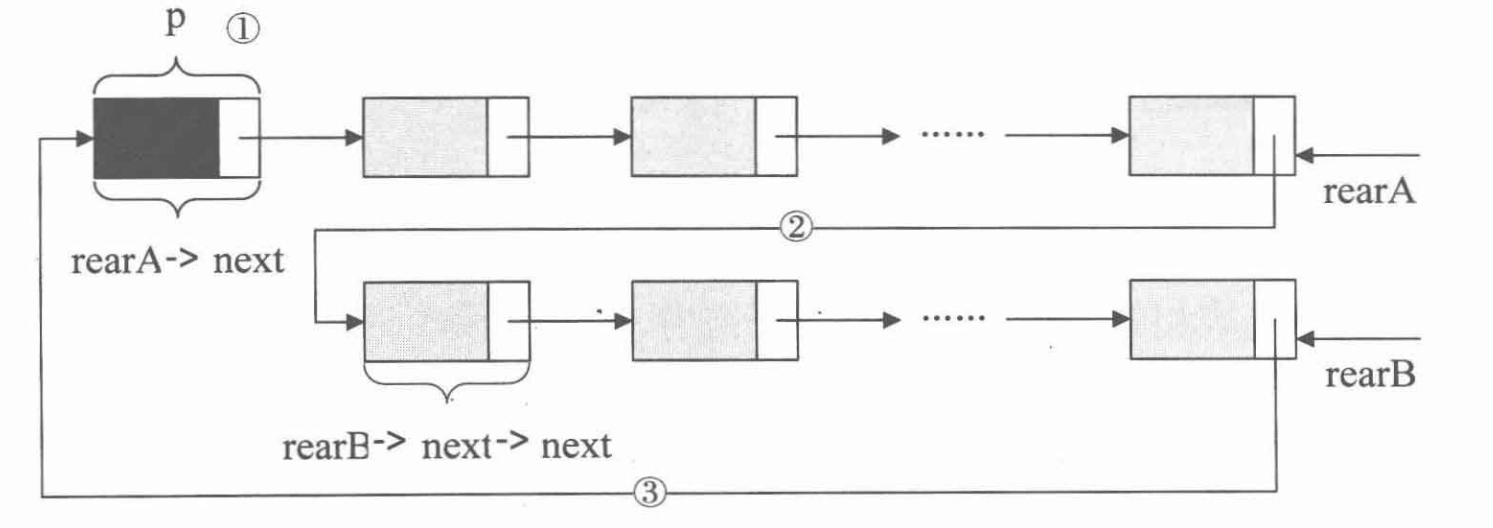
合并循环列表：

image-20220108151109520

要想实现合并操作，只需要进行下面的步骤就可以了：

image-20220108152039671
p = rearA->next;
q = rearB->next;
raarA->next = q->next;
rearB->next = p;
free(q);

栈

**栈( stack)是限定仅在表尾进行插入和删除操作的线性表。**我们把允许插入和删除的一端称为栈顶(top),另一端称为栈底( bottom),不含任何数据元素的栈称为空栈。栈又称为后进先出( Last In First Out)的线性表，简称LIFO结构。

栈的抽象数据类型定义如下：

ADT 栈（stack）
Data
	同线性表。元素具有相同的类型，相邻元素具有前驱和后继的关系。
Operation
	InitStack(*S): 初始化操作，建立一个空栈S。
	DestroyStack(*S): 若栈存在，则销毁它。
	ClearStack(*S): 将栈清空。
    StackEmpty(S): 栈为空则返回 true， 否则返回 false。
	GetTop(S,*e): 返回栈的栈顶元素 e。
    Push(*S, e): 插入元素 e 到栈顶。
    Pop(*S, *e): 弹出栈顶元素，并用 e 返回其值。
	StckLength(L): 返回 S 中的元素个数。
endADT

栈的顺序存储结构及其实现

typedef struct {
    ElemType data[MAXSIZE];
    int top;
}SqStack;

进栈操作

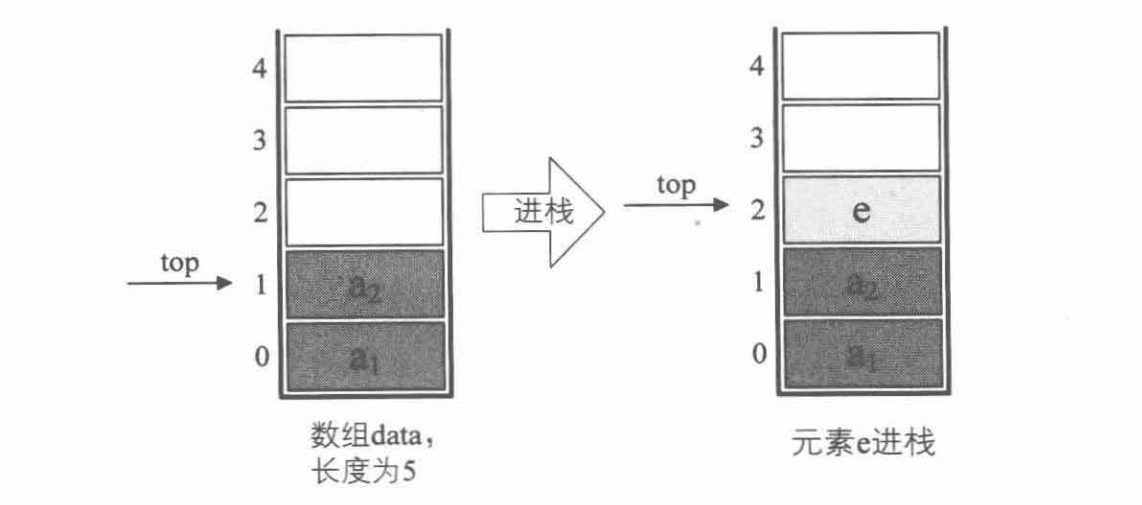
image-20220108154815946
// 将元素 e 插入栈中 ———— 进栈
Status Push(SqStack * S, ElemType e){
    // 如果栈满，返回 Error
    if(S->top == MAXSIZE - 1){
        return ERROR;
    }
    // 将 top ++，并将 top + 1赋值
    S->top++;
    S->data[S->top] = e;
    return OK;
}

出栈操作

Status Pop(SqStack *S, ElemType *e){
    if(S->top == -1){
        return ERROR;
    }
    // 将栈顶元素返回值给e，然后top--
    *e = S->data[S->top];
    S->top--;
    return OK;
}

栈的复用

采用如图所示的方式，两栈各自向中间靠拢：

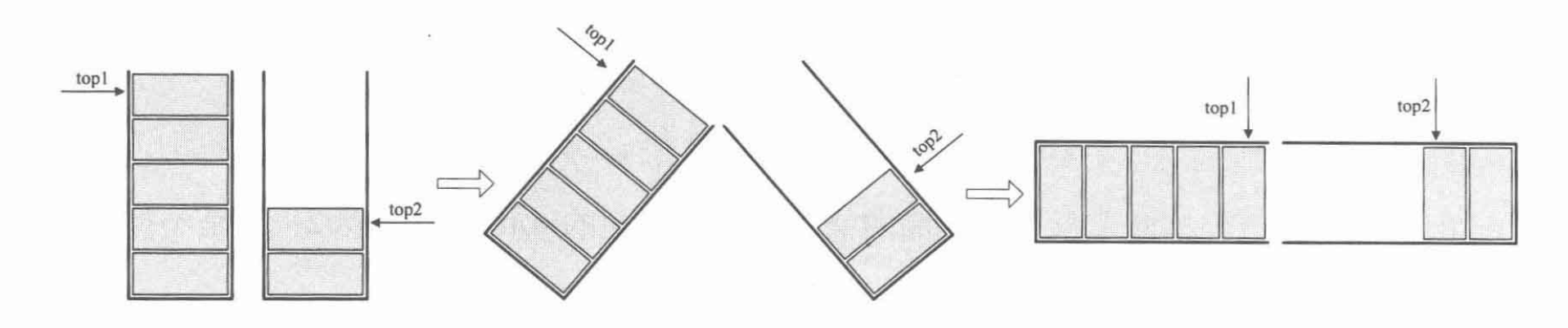
image-20220108155822895

存储结构：

typedef struct {
    ElemType data[MAXSIZE];
    int top1;
    int top2;
}SqDoubleStack;

插入元素：

Status Push(SqDoubleStack *S, ElemType e, int StackNumber){
    // 如果 top1 + 1 == top2 说明栈满
    if(S->top1 == S->top2 + 1){
        return ERROR;
    }
    if(StackNumber==1){
        S->top1++;
        S->data[S->top1] = e;
    }else if(StackNumber == 2){
        S->top2--;
        S->data[S->top2] = e;
    }
    return OK;
}

删除元素：

Status Pup(SqDoubleStack *S, ElemType *e, int StackNumber){
    if(StackNumber==1){
        // 如果 top1 == 0 说明栈空
        if(S->top1 == -1){
            return ERROR;
        }
        *e = S->data[S->top1];
        S->top1--;
    }else if(StackNumber == 2){
        // 如果 top2 == MAXSIZE 说明栈空
        if(S->top1 == MAXSIZE){
            return ERROR;
        }
        *e = S->data[S->top2];
        S->top2++;
    }
    return OK;
}

栈的链式存储结构及其实现

链栈的结构代码：

typedef struct StackNode{
    ElemType data;
    struct StackNode* next;
}StackNode, *LinkStackPtr;

typedef struct LinkStack{
    LinkStackPtr top;
    int count
}LinkStack;

进栈操作

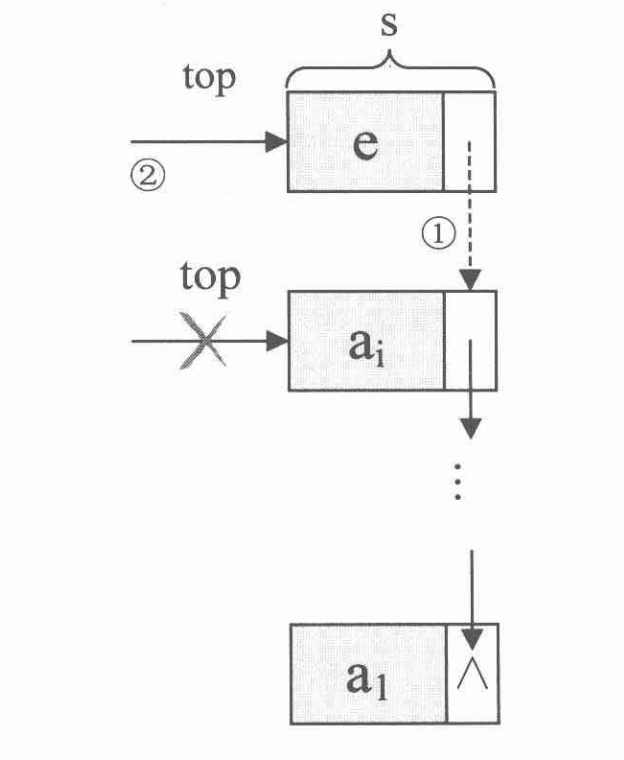
image-20220108162449416
Status Push(LinkStack * S, ElemType e){
    LinkStackPtr s = (LinkStackPtr) malloc(sizeof(StackNode));
    s->data = e;
    s->next = S->top;
    S->top = s;
    S->count++;
    return OK;
}

出栈操作

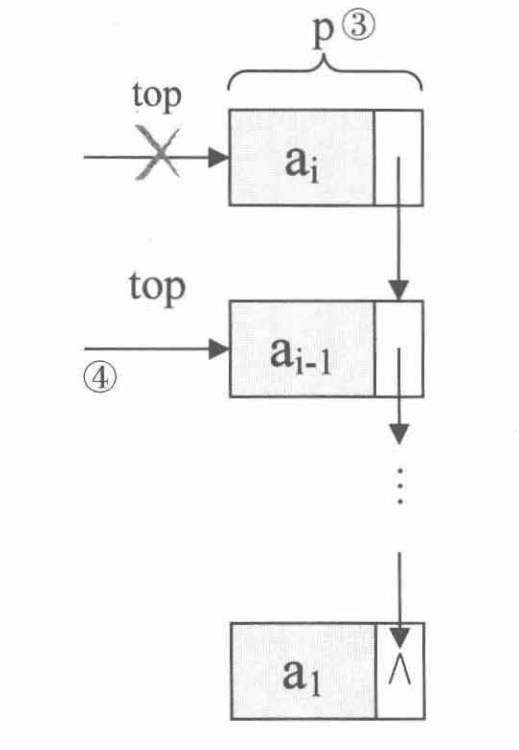
image-20220108162526207
Status Pop(LinkStack* S, ElemType*e){
    if(S->count == 0){
        return ERROR;
    }
    LinkStackPtr p = S->top;
    *e = p->data;
    S->top = p->next;
    free(p);
    S->count --;
    return OK;
}

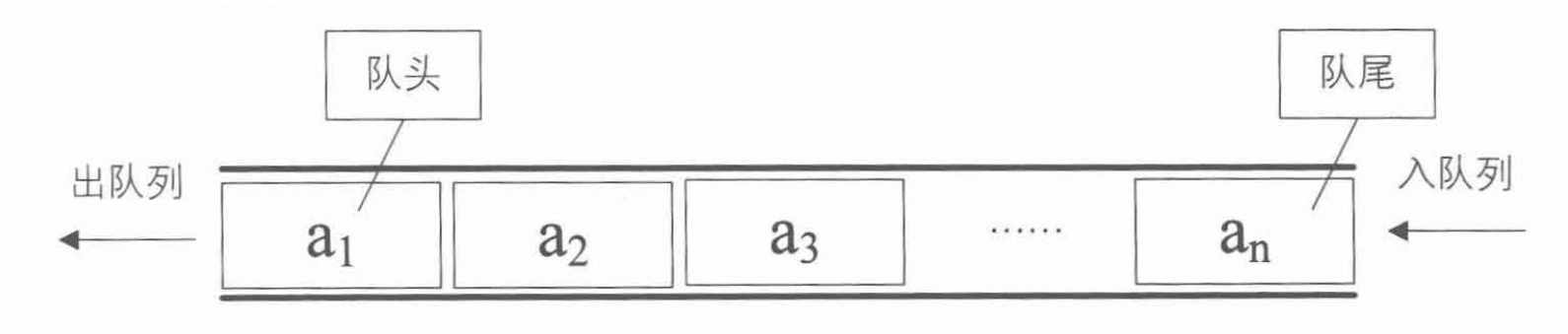
队列

**队列( queue)是只允许在一端进行插入操作，而在另一端进行删除操作的线性表。**队列是一种先进先出( First In First Out)的线性表，简称FIFO。允许插入的端称为队尾，允许删除的一端称为队头。

image-20220108165717337
ADT队列( Queue)
Data
	同线性表。元素具有相同的类型，相邻元素具有前驱和后继关系。
Operation
    Initqueue(*Q):初始化操作，建立一个空队列Q
    Destroyqueue(*Q):若队列Q存在，则销毁它。
    Clearqueue(E*Q):将队列Q清空。
    QueueEmpty(Q):若队列Q为空，返回true,否则返回false。
    GetHead(Q,*e):若队列Q存在且非空，用e返回队列Q的队头元素。
    Enqueue(*Q,e):若队列Q存在，插入新元素e到队列Q中并成为队尾元素。
    Dequeue(*Q,*e):删除队列Q中队头元素，并用e返回其值。
    Queuelength(Q):返回队列Q的元素个数
endadt

队列的顺序存储结构

image-20220108201009666

循环队列

存储结构代码：

typedef struct {
    ElemType data[MAXSIZE];
    int front; // 头指针
    int rear; // 尾指针，指向队尾的下一个元素
}SqQueue;

循环队列的初始化

Status InitQueue(SqQueue* Q){
    Q->front = 0;
    Q->rear = 0;
    return OK;
}

判断队列是否满

在判断是否已经满了的时候可以采用两种办法：

  • 空队列时， front等于rear,现在当队列满时，也是 front等于rear,那么如何判断此时的队列究竟是空还是满呢？
  • 办法一是设置一个标志变量 tag ,当font==rear,且tag=0时为队列空，当font==rear,且tag=1时为队列满
  • 办法二是当队列空时，条件就是 front=rear,当队列满时，我们修改其条件，保留一个元素空间。也就是说，队列满时，数组中还有一个空闲单元。

在方法二中：

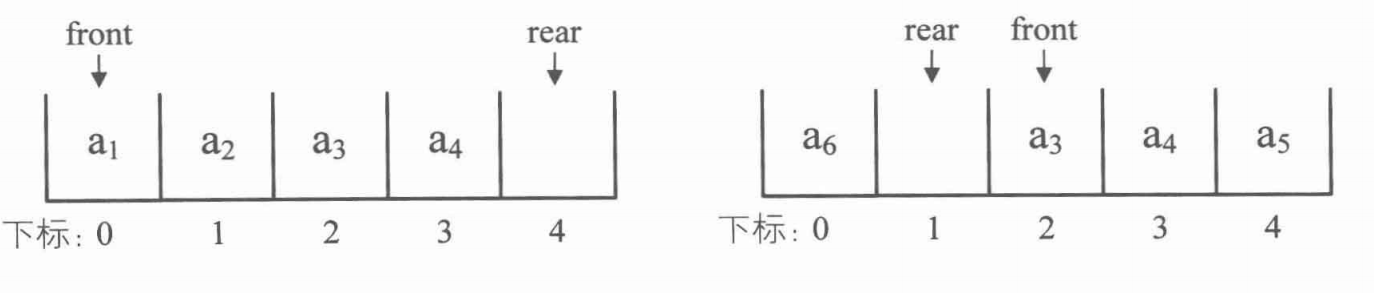
image-20220108195647383

可能会遇见上图中的两种情况，则判断队列是否为满的条件是：(rear+1)%MAXSIZE == front

求队列的长度

// 求循环队列的长度
int QueueLength(SqQueue Q){
    return (Q.rear - Q.front + MAXSIZE)%MAXSIZE;
}

入队

// 入队
Status EnQueue(SqQueue* Q, ElemType e){
    // 如果队满返回 ERROR
    if((Q->rear+1)%MAXSIZE == Q->front){
        return ERROR;
    }
    Q->data[Q->rear] = e;
    // 尾指针向后移动一位
    Q->rear = (Q->rear+1)%MAXSIZE;
    return OK;
}

出队

// 出队
Status DeQueue(SqQueue *Q, ElemType* e){
    // 如果队空，返回 ERROR
    if(Q->front == Q->rear){
        return ERROR;
    }
    *e = Q->data[Q->front];
    // 头指针向后移动一位
    Q->front = (Q->front + 1)% MAXSIZE;
    return OK;
}

队列的链式存储结构

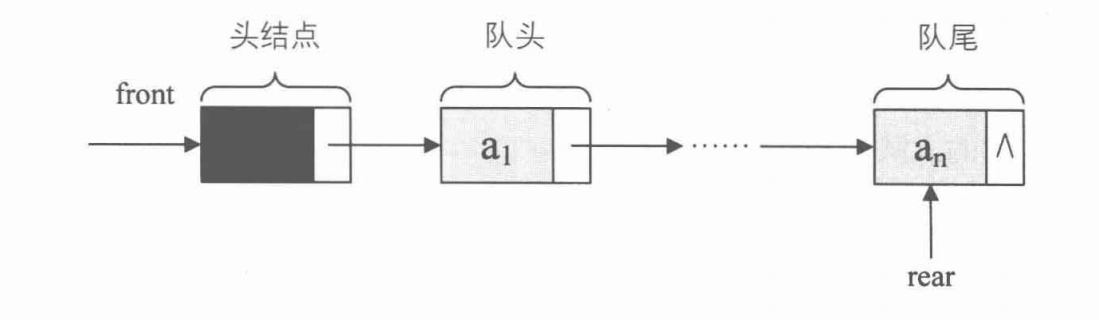
image-20220108201215973

队列的链式存储结构，其实就是线性表的单链表，只不过它只能尾进头出而已，我们把它简称为链队列。

存储结构代码：

typedef struct QNode{
    ElemType data;
    struct QNode* next;
}QNode, *QueuePtr;

typedef struct {
    QueuePtr front, rear;
}LinkQueue;

入队操作

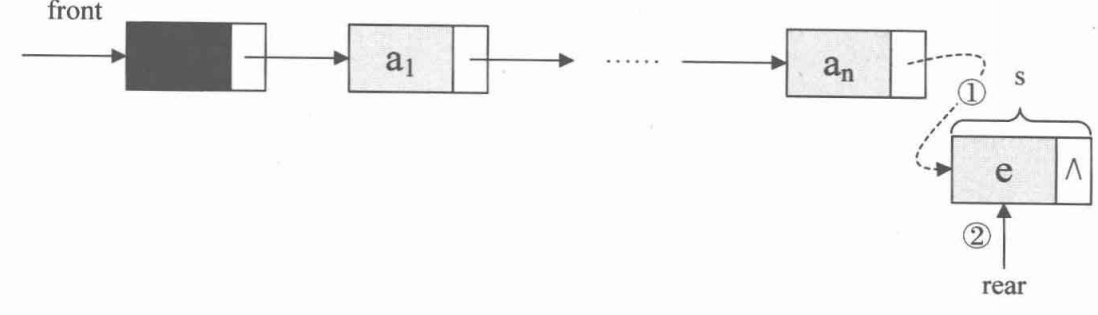
image-20220108201745057
Status EnQueue(LinkQueue *Q, ElemType e){
    // 创建 s 结点
    QueuePtr s = (QueuePtr) malloc(sizeof(QNode));
    s->data = e;
    s->next = NULL;
    // 将尾结点连上 s 结点，并将尾结点向后移动一位
    Q->rear->next = s;
    Q->rear = s;
    return OK;
}

出队操作

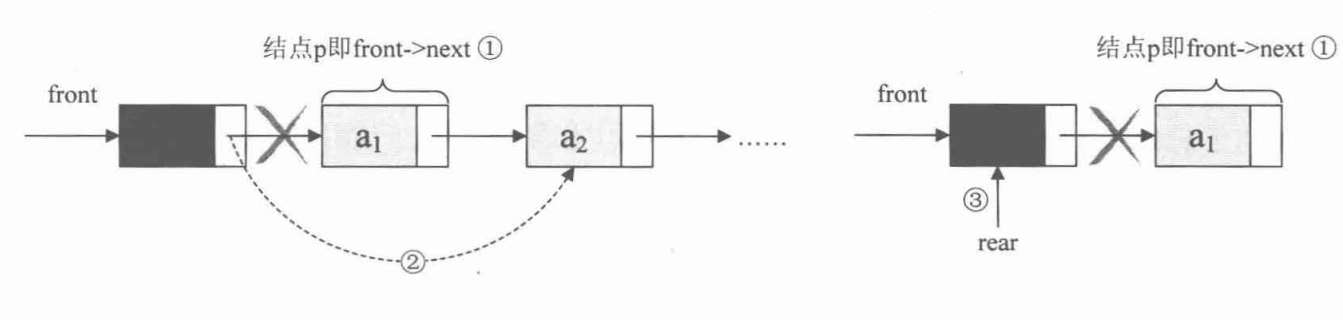
image-20220108201804055
Status DeQueue(LinkQueue* Q, ElemType* e){
    // 判断是否为空
    if(Q->rear == Q->front){
        return ERROR;
    }
    // 1. 获取第一个元素结点 2. 赋值给 e 3. 将头结点连上第二个结点 4. 释放原第一元素结点空间
    QueuePtr p = Q->front->next;
    *e = p->data;
    Q->front->next = p->next;
    // 若队头是队尾，删除后，将队尾指向头结点，见上图
    if(p == Q->rear){
        Q->rear = Q->front;
    }
    free(p);
    return OK;
}

串

串( string)是由零个或多个字符组成的有限序列，又名叫字符串。

串的抽象数据类型：

ADT	串(string)
Data
	串中元素仅由一个字符组成，相邻元素具有前驱和后继关系。
Operation
	StrAssign(T,* chars):生成一个其值等于字符串常量 chars的串T。
    StrCopy(T,S):串S存在，由串S复制得串T。
	ClearString(S):串S存在，将串清空。
	StringEmpty(S):若串S为空，返回true,否则返回 false。
	StrLength(S):返回串S的元素个数，即串的长度。
	StrCompare(S,T):若S>T,返回值>0,若S=T,返回0,若S<m,返回值<0。
	Concat(T,S1,S2):用T返回由S1和S2联接而成的新串。
	Substring(Sub,S,pos,len):串S存在，用Sub返回串S的第pos个字符起长度为1en的子串。
	Index(S,T,pos):串S和T存在，T是非空串，若主串S中存在和串值相同的子串，则返回它在主串S中第pos个字符之后第一次出现的位置，否则返回0。
	Replace(S,T,V):串S、T和V存在，T是非空串。用V替换主串S中出现的所有与T相等的不重叠的子串。
	StrInsert(S,pos,T):串S和T存在，在串S的第pos个字符之前插入串T。
	StrDelete(s,pos,len):串S存在，从串S中删除第pos个字符起长度为1en的子串。
ENDADT

串的比较

串的比较

给定两个串: s= a1 a2⋯⋯ a ns= \ {a}_{1} \ {a}_{2} \cdots \cdots \ {a}_{\ {n}} ,  t=b 1 b 2⋯⋯ b m\ {t}= {b}_{\ {1}} \ {b}_{\ {2}} \cdots \cdots \ {b}_{\ {m}} , 当满足以下条件之一时,  s< t\ {s}<\ {t} 。

  1.  n< m\ {n}<\ {m}, 且  a i= b i( i= 1,2,⋯⋯ , n)\ {a}_{\ {i}}=\ {b}_{\ {i}}(\ {i}=\ {1}, 2, \cdots \cdots, \ {n}) 。

例如当 s=s= “hap", t=t= “happy”, 就有 s<ts<t 。因为 tt 比 ss 多出了两个字母。

  1. 存在某个  k⩽ min( m, n)\ {k} \leqslant \ {m i n}(\ {m}, \ {n}), 使得  a i= b i\ {a}_{\ {i}}=\ {b}_{\ {i}} （  i= 1,2,⋯⋯ , k− 1\ {i}=\ {1}, 2, \cdots \cdots, \ {k}-\ {1} ),  a k< b k\ {a}_{\ {k}}<\ {b}_{\ {k}} 。

例如当 s=s= “happen”, t=t= “happy”, 因为两串的前 4 个字母均相同, 而两串第 5 个字母 ( k\mathrm{k} 值), 字母 e\mathrm{e} 的 ASCII 码是 101, 而字母 y\mathrm{y} 的 ASCII 码是 121, 显然 e<y\mathrm{e}<\mathrm{y}, 所以 s<t\mathrm{s}<\mathrm{t} 。

只有当两个串的长度和它们各个位置对应的字符都相等时，才算相等。

串的顺序存储结构

typedef struct{
    char str[MAXSIZE];
    int len;
}SqString;

串的链式存储结构

typedef struct Node{
    char data;
    struct Node* next;
}SNode;