跳至主要內容

灰色预测模型

CK...大约 11 分钟建模算法灰色预测预测类算法数学建模

灰色预测模型

模型基本介绍

灰色预测模型是通过少量的、不完全的信息，建立数学模型做出预测的一种预测方法。

基于客观事物的过去和现在的发展规律，借助于科学的方法对未来的发展趋势和状况进行描述和分析，并形成科学的假设和判断。

对于时间序列短，统计数据少，信息不完全系统的分析与建模，具有独特的功效

  • 既含有已知信息又含有未知信息的系统：灰色系统
  • 完全已知：白色系统
  • 完全位置：黑色系统

下面将介绍有关模型的几个相关概念

灰色生成数列

将原始数据列中的数据，按某种要求作数据处理称为生成。

灰色系统理论认为，尽管客观表象复杂，但总是有整体功能的，因此必然蕴含某种内在规律。关键在于如何选择适当的方式去挖掘和利用它。灰色系统时通过对原始数据的整理来寻求其变化规律的，这是一种就数据寻求数据的现实规律的途径，也就是灰色序列的生成。一切灰色序列都能通过某种生成弱化其随机性，显现其规律性。

  • 常用的灰色系统生成方式有:  （1）累加生成 （2）累减生成 （3）均值生成 （4）级比生成

累加生成

累加生成，即通过数列间各时刻数据的依个累加以得到新的数据与数列.累加前的数列称原始数列，累加后的数列称为生成数列.累加生成是使灰色过程由灰变白的一种方法，它在灰色系统理论中占有极其重要地位，通过累加生成可以看出灰量积累过程的发展态势,使离乱的原始数据中蕴含的积分特性或规律加以显化.累加生成是对原始数据列中各时刻的数据依次累加，从而生成新的序列的一种手段.

记原始序列为：

X(0)=(x(0)(1),x(0)(2),…….,x(0)(n)) X^{(0)}=\left(x^{(0)}(1), x^{(0)}(2), \ldots \ldots ., x^{(0)}(n)\right)

一次累加生成序列为:

X(1)=(x(1)(1),x(1)(2),…….,x(1)(n)) X^{(1)}=\left(x^{(1)}(1), x^{(1)}(2), \ldots \ldots ., x^{(1)}(n)\right)

其中:

x(1)(k)=∑i=0kx(0)(i)=x(1)(k−1)+x(0)(k) x^{(1)}(k)=\sum_{i=0}^{k} x^{(0)}(i)=x^{(1)}(k-1)+x^{(0)}(k)

举例：

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

累减生成

累减生成数实质是累加生成数的逆运算。 记原始序列为：

X(1)=(x(1)(1),x(1)(2),……,x(1)(n)) X^{(1)}=\left(x^{(1)}(1), x^{(1)}(2), \ldots \ldots, x^{(1)}(n)\right)

一次累减生成序列 1-IAGO:

X(0)=(x(0)(1),x(0)(2),……,x(0)(n)) X^{(0)}=\left(x^{(0)}(1), x^{(0)}(2), \ldots \ldots, x^{(0)}(n)\right)

其中:

x(0)(k)=x(1)(k)+x(1)(k−1),k=2,3,……,n x^{(0)}(k)=x^{(1)}(k)+x^{(1)}(k-1), \quad k=2,3, \ldots \ldots, n

邻值生成

令 Z(1)\mathrm{Z}^{(1)} 为 X(1)\mathrm{X}^{(1)} 的紧邻均值 MEAN生成序列:

Z(1)=(z(1)(2),z(1)(3),…….,z(1)(n)) Z^{(1)}=\left(z^{(1)}(2), z^{(1)}(3), \ldots \ldots ., z^{(1)}(n)\right)

其中:

z(1)(k)=αx(1)(k)+(1−α)x(1)(k−1),k=2,3,……,n z^{(1)}(k)=\alpha x^{(1)}(k)+(1-\alpha) x^{(1)}(k-1), \quad k=2,3, \ldots \ldots, n

α\alpha 为生成系数，取0.5时，称生成的数列为均值生成数，也称等权邻值生成数。

GM（1，1）模型

GM （1,1） 模型是灰色系统理论中应用最广泛的一种灰色动态预测模型，该模型由一个单变量的一阶微分方程构成。 它主要用于复杂系统某一主导因素特征值的拟合和预测，以揭示主导因素变化规律和未来发展变化态势。

其中 G 代表 “Grey” M代表 “Model” （1，1）代表 1 阶方程 1 个变量

灰微分方程模型

定义灰导数：

d(k)=x(0)(k)=x(1)(k)−x(1)(k−1) d(k)=x^{(0)}(k)=x^{(1)}(k)-x^{(1)}(k-1)

这里 x(0)(k)k=1,2,...,3x^{(0)}(k)\qquad k=1,2,...,3 为原始数列

这里 x(1)(k)k=1,2,...,3x^{(1)}(k)\qquad k=1,2,...,3 为累加生成数列（见上文）

结合邻值生成序列，定义 GM(1,1)\mathrm{GM}(1,1) 灰微分方程模型为：

x(0)(k)+az(1)(k)=b x^{(0)}(k)+a z^{(1)}(k)=b

或

d(k)+az(1)(k)=b d(k)+a z^{(1)}(k)=b

这里 z(1)(k)k=1,2,...,3z^{(1)}(k)\qquad k=1,2,...,3 为邻值生成数列（见上文）

其中, a称为发展系数, z(1)(k)\mathrm{z}^{(1)}(\mathrm{k}) 称为白化背景值, b\mathrm{b} 称为灰作用量。 现 x(0)、z(1)(k)x^{(0)} \text{、} z^{(1)}(k) 为已知量, a、ba \text{、}b 待求解， 故将 k=2,3,…,nk=2,3, \ldots, \mathrm{n} 待入， 可得到矩阵方程

{x(0)(2)+az(1)(2)=b,x(0)(3)+az(1)(3)=b……,x(0)(n)+az(1)(n)=b \left\{\begin{array}{l} x^{(0)}(2)+a z^{(1)}(2)=b, \\ x^{(0)}(3)+a z^{(1)}(3)=b \\ \ldots \ldots, \\ x^{(0)}(n)+a z^{(1)}(n)=b \end{array}\right.

稍做转换：

{x(0)(2)=−az(1)(2)+b,x(0)(3)=−az(1)(3)+b,……,x(0)(n)=−az(1)(n)+b \left\{\begin{array}{l} x^{(0)}(2)=-a z^{(1)}(2)+b, \\ x^{(0)}(3)=-a z^{(1)}(3)+b, \\ \ldots \ldots, \\ x^{(0)}(n)=-a z^{(1)}(n)+b \end{array}\right.

令:

u=[ab]Y=[x(0)(2)x(0)(3)……x(0)(n)]B=[−z(1)(2)1−z(1)(3)1⋯⋯−z(1)(n)1] \begin{gathered} u=\left[\begin{array}{l} a \\ b \end{array}\right] \\ Y=\left[\begin{array}{c} x^{(0)}(2) \\ x^{(0)}(3) \\ \ldots \ldots \\ x^{(0)}(n) \end{array}\right] \\ B=\left[\begin{array}{cc} -z^{(1)}(2) & 1 \\ -z^{(1)}(3) & 1 \\ \cdots \cdots & \\ -z^{(1)}(n) & 1 \end{array}\right] \end{gathered}

此时, GM(1,1)\mathrm{GM}(1,1) 模型转化为 Bu=YBu=Y, 利用矩阵运算， 解得： u=YB−1u=YB^{-1}.

白化方程模型

定义：对于 GM(1,1)GM(1,1) 的灰微分方程，如果将时刻 k=2,3,…,nk=2,3,…,n 视为连续变量 tt，则之前的 x(1)x(1) 视为时间t函数，于是灰导数 x(0)(k)x^{(0)}(k) 变为连续函数的导数 dx(1)dt\cfrac{dx(1)}{dt} ，白化背景值 z(1)(k)z^{(1)}(k) 对应于导数 x(1)(t)x^{(1)}(t)。于是 GM（1，1）的灰微分方程对应于的白微分方程为：

dx(1)(t)dt+ax(1)(t)=b \frac{d x^{(1)}(t)}{d t}+a x^{(1)}(t)=b

解为：

x(1)(t)=(x(0)(1)−ba)e−a(t−1)+ba x^{(1)}(t)=\left(x^{(0)}(1)-\frac{b}{a}\right) e^{-a(t-1)}+\frac{b}{a}

注意：此处得到的解为累加数列，后续需要将其转化为累减数列

算法步骤

1. 数据的检验与处理

为了保证GM （1,1） 建模方法的可行性，需要对已知数据做必要的检验处理。 计算数列的级比：

λ(k)=x(0)(k−1)x(0)(k),k=2,3,…,n \lambda(k)=\frac{x^{(0)}(k-1)}{x^{(0)}(k)}, k=2,3, \ldots, n

通过范围: (e−2/(n+1),e2/(n+2))\quad\left(\mathrm{e}^{-2 /(\mathrm{n}+1)}, \mathrm{e}^{2 /(\mathrm{n}+2)}\right) 否则需要对数列作平移变换，使级比落在范围中

y(0)(k)=x(0)(k)+C,k=1,2,…,n y^{(0)}(k)=x^{(0)}(k)+C, k=1,2, \ldots, n

2. 建立模型，求出预测值

通过灰微分方程建立：

x(0)(k)+az(1)(k)=b x^{(0)}(k)+a z^{(1)}(k)=b

代入相关值求解得到 a，b。

建立白化微分方程：

dx(1)(t)dt+ax(1)(t)=b \frac{d x^{(1)}(t)}{d t}+a x^{(1)}(t)=b

通过对白化方程的解，进行累减，得到预测值。

x(1)(t)=(x(0)(1)−ba)e−a(t−1)+bax^(1)(k+1)=(x(0)(1)−ba)e−ak+bax^(0)(k)=x^(1)(k)+x^(1)(k−1),k=2,3,……,n \begin{gathered} x^{(1)}(t)=\left(x^{(0)}(1)-\frac{b}{a}\right) e^{-a(t-1)}+\frac{b}{a} \\ \hat{x}^{(1)}(k+1)=\left(x^{(0)}(1)-\frac{b}{a}\right) e^{-a k}+\frac{b}{a} \\ \hat{x}^{(0)}(k)=\hat{x}^{(1)}(k)+\hat{x}^{(1)}(k-1), \quad k=2,3, \ldots \ldots, n \end{gathered}

3. 检验预测值

方法一：

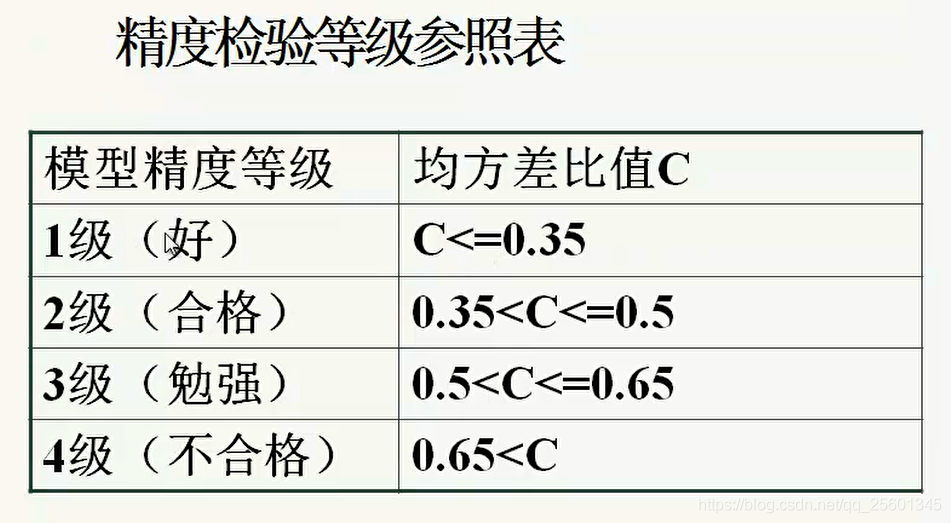
在这里插入图片描述在这里插入图片描述在这里插入图片描述在这里插入图片描述

方法二：

  • 计算相对残差

ξk=x(0)(k)−x^(0)(k)x(0)(k) \xi_{k}=\frac{x^{(0)}(k)-\hat{x}^{(0)}(k)}{x^{(0)}(k)}

若所有的 ∣ξk∣<0.1\left|\xi_{k}\right|<0.1, 则认为达到较高的要求;

若所有的 ∣ξk∣<0.2\left|\xi_{k}\right|<0.2 ， 则认为达到一般的要求。

  • 级比偏差值检验

ρ(k)=1−1−0.5a1+0.5aλ(k) \rho(k)=1-\frac{1-0.5 a}{1+0.5 a} \lambda(k)

若所有的 ρ(k)∣<0.1\rho(k) \mid<0.1, 则认为达到较高的要求;

若所有的 ρ(k)∣<0.2\rho(k) \mid<0.2 ， 则认为达到一般的要求。

Matlab 编程实现

%（1）输入前期的小样本数据
%（2）输入预测个数
%（3）运行
y=input('请输入数据');
n=length(y);
yy=ones(n,1);
yy(1)=y(1);
for i=2:n
    yy(i)=yy(i-1)+y(i)
end
B=ones(n-1,2);
for i=1:(n-1)
    B(i,1)=-(yy(i)+yy(i+1))/2;
    B(i,2)=1;
end
BT=B';
for j=1:(n-1)
    YN(j)=y(j+1);
end
YN=YN';
A=inv(BT*B)*BT*YN;
a=A(1);
u=A(2);
t=u/a;
t_test=input('输入需要预测的个数');
i=1:t_test+n;
yys(i+1)=(y(1)-t).*exp(-a.*i)+t;
yys(1)=y(1);
for j=n+t_test:-1:2
    ys(j)=yys(j)-yys(j-1);
end
x=1:n;
xs=2:n+t_test;
yn=ys(2:n+t_test);
plot(x,y,'^r',xs,yn,'*-b');
det=0;
for i=2:n
    det=det+abs(yn(i)-y(i));
end
det=det/(n-1);
disp(['百分绝对误差为：',num2str(det),'%']);
    disp(['预测值为：',num2str(ys(n+1:n+t_test))]);

应用实例（重要！！）

灰色预测计算实例

**例：**北方某城市 1986～1992 年道路交通噪声平均声级数据见表，请预测后几年的平均噪声：

序号年份LeqL_{eq}序号年份LeqL_{eq}
1198671.15199071.4
2198772.46199172.0
3198872.47199271.6
4198972.1

解：

第一步：级比检验 建立交通噪声平均声级数据时间序列如下：

x(0)=(x(0)(1),x(0)(2),⋯ ,x(0)(7))=(71.1,72.4,72.4,72.1,71.4,72.0,71.6) \begin{aligned} x^{(0)} &=\left(x^{(0)}(1), x^{(0)}(2), \cdots, x^{(0)}(7)\right) \\ &=(71.1,72.4,72.4,72.1,71.4,72.0,71.6) \end{aligned}

（1）求级比 λ(k)\lambda(k)

λ(k)=x(0)(k−1)x(0)(k) \lambda(k)=\frac{x^{(0)}(k-1)}{x^{(0)}(k)}

λ=(λ(2),λ(3),⋯ ,λ(7))=(0.982,1,1.0042,1.0098,0.9917,1.0056) \begin{aligned} \lambda &=(\lambda(2), \lambda(3), \cdots, \lambda(7)) \\ &=(0.982,1,1.0042,1.0098,0.9917,1.0056) \end{aligned}

（2）级比判断 由于所有的 λ(k)∈[0.982,1.0098],k=2,3,⋯ ,7\lambda(k) \in[0.982,1.0098], k=2,3, \cdots, 7, 故可以用 x(0)x^{(0)} 作满意的GM（1，1）建模。

第二步: GM（1,1） 建模 （1） 对原始数据 x(0)x^{(0)} 作一次累加，即 x(1)=(71.1,143.5,215.9,288,359.4,431.4,503)x^{(1)}=(71.1,143.5,215.9,288,359.4,431.4,503) （2） 构造数据矩阵 BB 及数据向量 YY

B=[−12(x(1)(1)+x(1)(2))1−12(x(1)(2)+x(1)(3))1⋮⋮−12(x(1)(6)+x(1)(7))1],Y=[x(0)(2)x(0)(3)⋮x(0)(7)] B=\left[\begin{array}{cc} -\frac{1}{2}\left(x^{(1)}(1)+x^{(1)}(2)\right) & 1 \\ -\frac{1}{2}\left(x^{(1)}(2)+x^{(1)}(3)\right) & 1 \\ \vdots & \vdots \\ -\frac{1}{2}\left(x^{(1)}(6)+x^{(1)}(7)\right) & 1 \end{array}\right], \quad Y=\left[\begin{array}{c} x^{(0)}(2) \\ x^{(0)}(3) \\ \vdots \\ x^{(0)}(7) \end{array}\right]

（3）计算 u^\hat{u}

u^=(a,b)T=(BTB)−1BTY=(0.002372.6573) \hat{u}=(a, b)^{T}=\left(B^{T} B\right)^{-1} B^{T} Y=\left(\begin{array}{l} 0.0023 \\ 72.6573 \end{array}\right)

于是得到 a=0.0023,b=72.6573a=0.0023, b=72.6573 。 （4）建立模型

dx(1)dt+0.0023x(1)=72.6573 \frac{d x^{(1)}}{d t}+0.0023 x^{(1)}=72.6573

求解得

x(1)(k+1)=(x(0)(1)−ba)e−ak+ba=−30929e−0.0023k+31000 x^{(1)}(k+1)=\left(x^{(0)}(1)-\frac{b}{a}\right) e^{-a k}+\frac{b}{a}=-30929 e^{-0.0023 k}+31000

（5） 求生成数列预测值 x^(1)(k+1)\hat{x}^{(1)}(k+1) 及模型还原值 x^(0)(k+1)\hat{x}^{(0)}(k+1) :

令 k=1,2,3,4,5,6k=1,2,3,4,5,6, 由上面的时间响应函数可算得 x^(1)\hat{x}^{(1)}, 其中取

x^(1)(1)=x^(0)(1)=x(0)(1)=71.1 由 x^(0)(k)=x^(1)(k)−x^(1)(k−1), 取 k=2,3,4,⋯ ,7, 得 x^(0)=(x^(0)(1),x^(0)(2),⋯ ,x^(0)(7))=(71.1,72.4,72.2,72.1,71.9,71.7,71.6) \begin{aligned} &\hat{x}^{(1)}(1)=\hat{x}^{(0)}(1)=x^{(0)}(1)=71.1\\ &\text { 由 } \hat{x}^{(0)}(k)=\hat{x}^{(1)}(k)-\hat{x}^{(1)}(k-1), \text { 取 } k=2,3,4, \cdots, 7, \text { 得 }\\ &\hat{x}^{(0)}=\left(\hat{x}^{(0)}(1), \hat{x}^{(0)}(2), \cdots, \hat{x}^{(0)}(7)\right)=(71.1,72.4,72.2,72.1,71.9,71.7,71.6) \end{aligned}

第三步：模型检验

模型检验结果见下表：

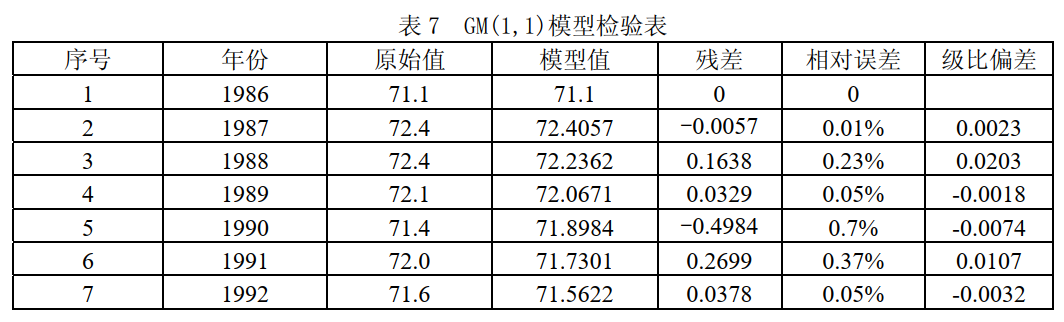image-20210706234416610
image-20210706234416610

经检验符合标准。

灾变预测

给定原始数据列 x(0)=(x(0)(1),x(0)(2),⋯ ,x(0)(n))x^{(0)}=\left(x^{(0)}(1), x^{(0)}(2), \cdots, x^{(0)}(n)\right) 。 如果指定某个定值 ζ\zeta, 并认 为 x(0)x^{(0)} 中那些大于 ζ\zeta 的点为具有异常值的点，然后将这些数据挑出来另组一数列，则 称这一数列为上限灾变数列。例如，给定数列 x(0)=(3,0.7,8,5)x^{(0)}=(3,0.7,8,5), 若取 ζ=1\zeta=1, 则其上 限灾变数列为

xζ0=(3,8,5) x_{\zeta}^{0}=(3,8,5)

同理, 可定义下限灾变数列这个概念。注意，灾变预测不是预测数据本身的大小, 而是预测异常值出现的时间。我们考虑下面这个问题。

例： 某地区年均降雨量数据如表所示 。规定 ζ=320\zeta = 320 ，并认为 x(0)(i)≤ζx^{(0)}(i) \le \zeta 为旱灾。预测下一次旱灾发生的时间。

image-20210706231338595
image-20210706231338595

解：

写出初始数列

x(0)=(390.6,412,320,559.2,380.8,542.4,553,310,561,300,632,540,406.2,313.8,576,587.6,318.5) \begin{gathered} x^{(0)}=(390.6,412,320,559.2,380.8,542.4,553,310,561,300,632, \\ 540,406.2,313.8,576,587.6,318.5) \end{gathered}

由于满足 x(0)(i)≤320x^{(0)}(i) \leq 320 的 x(0)(i)x^{(0)}(i) 即为异常值, 易得下限灾变数列为

xζ0=(320,310,300,313.8,318.5) x_{\zeta}^{0}=(320,310,300,313.8,318.5)

其对应的时刻数列为

t=(3,8,10,14,17) t=(3,8,10,14,17)

将数列 tt 做 1 次累加，得

t(1)=(3,11,21,35,52) t^{(1)}=(3,11,21,35,52)

建立 GM(1,1)\mathrm{GM}(1,1) 模型，得

u^=(a,b)T=(−0.2536,6.2585)t^(1)(k+1)=27.6774e0.2536k−24.6774 \begin{aligned} &\hat{u}=(a, b)^{T}=(-0.2536,6.2585) \\ &\hat{t}^{(1)}(k+1)=27.6774 e^{0.2536 k}-24.6774 \end{aligned}

通过上式, 预测到第 6 个及第 7 个数据为

t(0)(6)=22.034,t(0)(7)=28.3946 t^{(0)}(6)=22.034, \quad t^{(0)}(7)=28.3946

由于 22.03422.034 与 17 相差 5.0345.034, 这表明下一次旱灾将发生在五年以后。

模型评价

模型优点：

  • 所需建模信息少

  • 运算方便

  • 建模精度高

模型缺点：

对非线性数据样本预测效果差。

据了解，灰色系统 (Grey System)理论 是我国著名学者邓聚龙教授 20 世纪 80 年代初创立的一种兼备软硬科学特性的新理论。然而，在美国数学建模大赛中，基本不承认此模型，故需要回避使用。

参考博文及文献

【数学建模】灰色预测模型GM(1，1)附例题分析(MATLAB实现)open in new window

【数学建模】灰色预测模型（预测）open in new window

【数学建模】灰色预测模型open in new window

灰色预测模型open in new window

《数学建模算法与应用》------司守奎