基于深度优先搜索回溯法的人狼羊菜过河模型

CK...大约 14 分钟

基于深度优先搜索回溯法的人狼羊菜过河模型

提示

本文介绍一个农夫过河的小模型，算法 Python 实现，感觉还挺有趣的，因原为笔者课程作业论文改版而来，所以文章内容比起其他博客文章可能会比较严肃与严谨。期待与你的思维碰撞。

摘要

本文介绍了一种合理规划农夫携带狼、羊、菜安全过河问题。对问题合理分析，将人、狼、羊、菜四者的某时刻状态量化为一向量，基于此结构建立安全位置状态集合，与安全运输状态集合，存储运输过程中可能的位置状态与运输状态。以初始状态向量为起点，采用回溯法，深度优先遍历所有可行路径，将符合题目条件并未重复的可行路径添入历史路径集合中，并记录此时的位置状态。递归至搜索到终止状态集合，输出所有历史位置状态集合，即为一条可行方案。回溯弹出，即可搜寻到所有可行路径。并根据所搜寻到的可行路径输出最短路径。

通过上述模型及算法，本文基于 Python 语言，实现模型求解最终找到此问题唯二解：

农夫带羊过河 $\rightarrow$ 农夫返回 $\rightarrow$ 农夫带狼过河 $\rightarrow$ 农夫带羊返回 $\rightarrow$ 农夫带菜过河 $\rightarrow$ 农夫返回 $\rightarrow$ 农夫带羊过河
农夫带羊过河 $\rightarrow$ 农夫返回 $\rightarrow$ 农夫带菜过河 $\rightarrow$ 农夫带羊返回 $\rightarrow$ 农夫带狼过河 $\rightarrow$ 农夫返回 $\rightarrow$ 农夫带羊过河

为检验模型的正确性与普适性，本文假定当狼、羊同时存在时（农夫不存在），狼不会吃羊。即添加两安全位置状态向量。得到更改后问题的唯八解（见正文），并且所得到的最短路径更少。验证模型准确性高，具有普适性。拓展到日常生活的规划问题时，具有一定的参考意义。

关键字: 回溯法深度优先搜索DFS 空间状态树 Python

问题重述

问题描述

本文致力于解决一位农夫的过河问题。在此问题中，一位农夫，携带狼、羊、菜，准备过河，在只有一艘船只且每次过河农夫只能携带狼、羊、菜其中一件个体的前提下，保证农夫与每件个体安全渡河。而在过河过程中，由于缺少农夫的看管，当狼与羊单独在一岸时，狼可以吃羊使得渡河失败；由于缺少农夫的看管，当羊与菜单独在一岸时，羊可以吃菜使得渡河失败。如何让狼、羊、菜同时保证安全的前提下，让农夫顺利过河，取决于农夫每次过河时所携带的个体。本文建立合适的模型，并选择合适的算法，寻找所有的渡河决策。

这个问题属实离谱，《养狼的农夫》，而且农夫还没有绳子可以把羊和狼拴起来，哎大家别较真。

问题要求

在此问题中的求解中，需要满足下列条件：

保证狼与羊不单独在同一岸边；
保证羊与菜不单独在同一岸边；
农夫每次运输只能携带狼、羊、菜中的一位，或者不携带其中的任何一位；
决策需要在有限次完成，并保证前后互不重复。

在保证狼、羊、菜全部安全的前提下，建立合适模型，并选择合适算法求解，找出决策变化规律。寻找到所有有限次符合要求的农夫渡河决策。

问题分析

在此问题中，由于对狼、羊、菜相关约束条件，为保证每一件个体的安全，不单独将狼与羊或羊与菜放在同一岸边，对于这一人、狼、羊、菜四者的所在位置状态的约束，考虑河岸的任意一边，通过穷举，不难想出，各河岸有且仅有下面的十种安全位置状态（如下表所示），由对称性，另一边的安全位置状态与此相同。

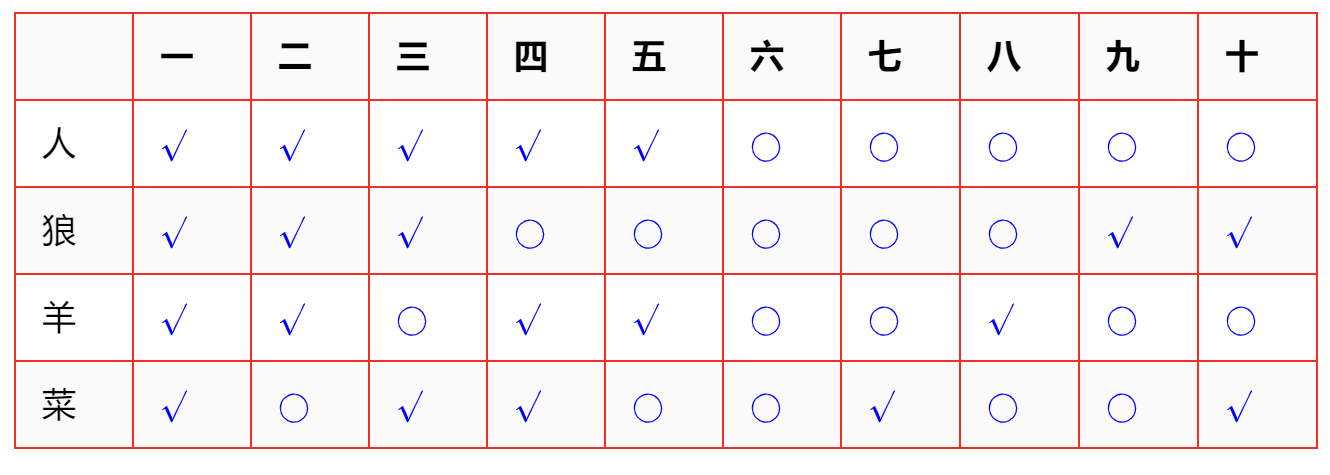
在此问题中，由于农夫和小船运输限制，每次渡河农夫必须在船上，并且农夫可以选择携带狼、羊、菜中的任何一个，当然农夫可以选择不携带其中的任何一个，而单独过河。在上述情况中，通过穷尽，不难想出，每次渡河，从河的一边运输到另外一边，在运输船中，有且仅有下面四种运输状态（如下表所示），由对称性，从河的另一岸到此岸的运输状态相同。

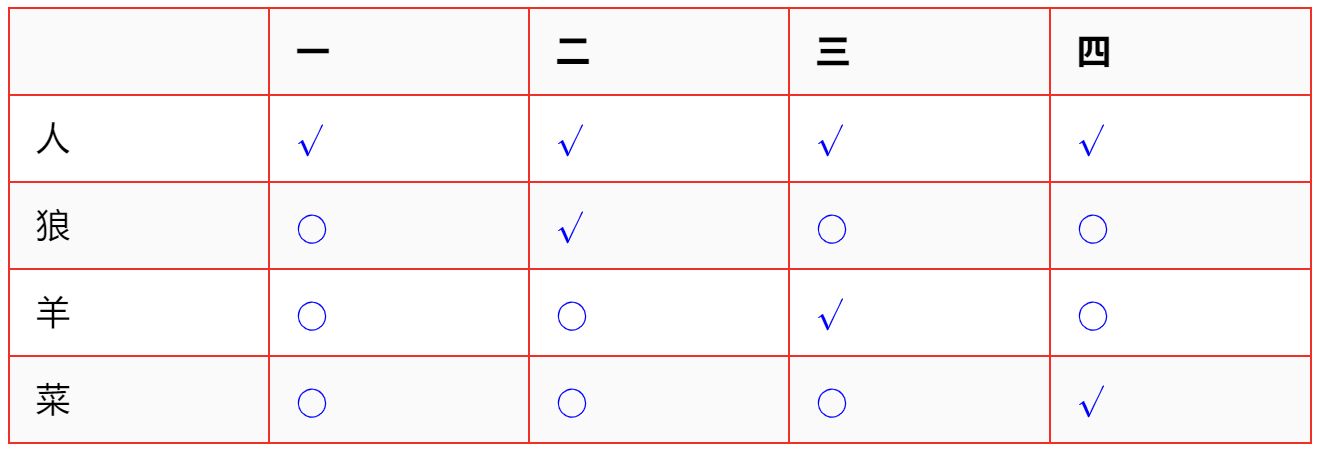
问题的起始状态为：人、狼、羊、菜在此岸，而本文所要寻找的决策便是由一系列的人狼羊菜安全运输状态组成，使最终的人狼羊菜位置状态为：人、狼、羊、菜在彼岸。

注：其中 $\surd$ 表示存在， $\bigcirc$ 表示不存在。

为合理量化模型状态，本文采用二进制向量数据结构，四位向量数据因子分布存储人、狼、羊、菜的位置状态与运输状态：

位置状态：每个个体所处位置状态仅有两种情况，在此岸与未在此岸，设定 1 为在此岸， 0 为位未在此岸；
运输状态：每个个体所处运输状态仅有两种情况，被运输与未被运输，设定 1 为被运输， 0 为未被运输。

搜寻可行路径，使得每次状态向量均为安全状态向量。状态起点为 $(1,1,1,1)$ ，当搜寻至状态终点 $(0,0,0,0)$ 时，成功完成渡河，即为所搜索到的一条运输策略。记录运输策略集合中所包含的状态向量个数。则最短路径即为当包含的状态向量个数最少时的最优解。

##　名词解释与模型假设

名词解释

本文部分所用具体符号如下表所示：

符号表示	说明
集合 $S_k\quad \{k=1,2,...,10\}$	人狼羊菜安全位置状态集合
集合 $M_k\quad \{k=1,2,3,4\}$	人狼羊菜安全运输状态集合
集合 $G_k \quad \{k=1,2,...,n\}$	历史位置状态集合
集合 $H_k \quad \{k=1,2,...,m\}$	历史运输状态集合

模型假设

为使所建立模型更加合理，避免异常情况干扰模型结果，在满足客观条件下，设定下面的模型假设：

运输过程，不因时间或利益成本而丢弃或放弃任意一件个体；
当狼、羊单独存在时，假设二者不会自主逃跑或丢失；
每次运输过程除运输个体外，环境条件完全相同，不考虑风浪及农夫体力对运输的影响；
农夫所养之狼并不会出现恶意攻击农夫或不服从农夫命令的行为。

模型的建立与求解

模型的建立

为合理量化模型状态，本文采用二进制向量数据结构，四位向量数据因子分布存储人、狼、羊、菜的位置状态与运输状态：

位置状态：每个个体所处位置状态仅有两种情况，在此岸与未在此岸，设定 1 为在此岸， 0 为位未在此岸；
运输状态：每个个体所处运输状态仅有两种情况，被运输与未被运输，设定 1 为被运输， 0 为未被运输。

由此结构，可将安全位置状态集合量化如下：

S = \begin{cases} (1, 1, 1, 1)\quad (1, 1, 1, 0)\quad (1, 1, 0, 1)\quad (1, 0, 1, 1)\quad (1, 0, 1, 0)\\ (0, 0, 0, 0)\quad(0, 0, 0, 1)\quad (0, 0, 1, 0)\quad (0, 1, 0, 0)\quad (0, 1, 0, 1) \end{cases}

可将安全运输状态集合量化如下：

M = \{ (1, 0, 0, 0)\quad (1, 1, 0, 0)\quad (1, 0, 1, 0)\quad (1, 0, 0, 1) \}

由位置状态及运输状态定义可知，满足下面条件：

G_{k+1} = G_{k} + H_{k}\\ G_{k},G_{k+1} \in S\\ H_{k} \in M

其中 $G_k \quad \{k=1,2,...,n\}$ 为历史位置状态集合，存储运输过程中符合条件的个体位置状态， $H_k \quad \{k=1,2,...,m\}$ 为历史运输状态集合，存储运输过程中符合条件的个体运输状态。并且一定有

m = n - 1

由于两种状态向量的特殊关系，对应状态向量因子之间的相加运算符合下列条件：

$ 1 + 1 = 0$，在此岸个体被运输去后，位置状态向量为 0，表示已不在此岸；
$1 + 0 = 1$ ，在此岸个体未被运输后，位置状态向量仍为 1，表示仍在此岸；
$0 + 1 = 1$ ，未在此岸个体被运输来后，位置状态为 1，表示来到此岸；
$0 + 0 = 0$ ，未在此岸个体未被运输后，位置状态仍为 0，表示仍未在此岸。

为避免所寻路径重复，需要补充条件：

G_{k} \notin G_{i} \qquad i < k

所建模型初始位置状态向量： $G_1=(1, 1, 1, 1)$ ，当模型满足上述 $(1),(2),(3),(4)$ 条件，并且搜寻到目标状态向量： $G_n=(0, 0, 0, 0)$ 时，成功完成渡河，所搜索到的运输策略即为

H_{k}\qquad \text{其中}k=1,2,...,n-1

记录 $m=n-1$ ，当全部搜索遍历结束后，取到$\min m $的路径集合即为最短路径方案。

考虑模型数据结构，基于此问题，由于面对同一状态向量下，可能有多个安全运输状态，有多种运输方法策略，本文用空间状态树，存储遍历搜索路径中的可行位置状态，故空间状态树的根节点为 $(0,0,0,0)$ ，当搜索到叶子节点为 $(1,1,1,1)$ 时，从根节点到该叶子节点的一条路径便是一条可行路径。

模型的求解

回溯法按深度优先策略搜索问题的解空间树。首先从根节点出发搜索解空间树，当算法搜索至解空间树的某一节点时，先利用剪枝函数判断该节点是否可行（即能得到问题的解）。如果不可行，则跳过对该节点为根的子树的搜索，逐层向其祖先节点回溯；否则，进入该子树，继续按深度优先策略搜索。

具体回溯步骤如下图流程图所示：

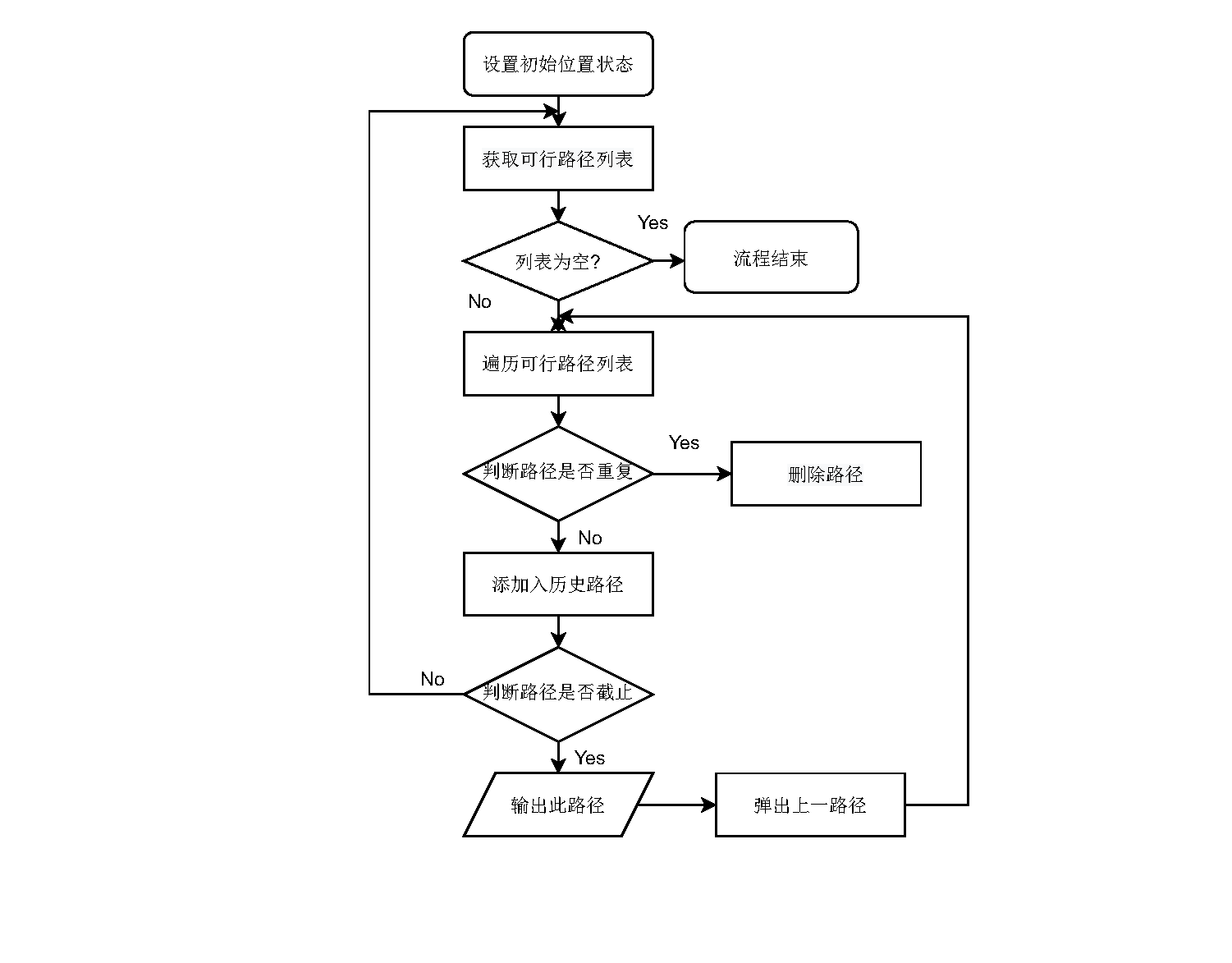
回溯法的基本行为是搜索，搜索过程使用剪枝函数来为了避免无效的搜索。剪枝函数包括两类：1. 使用约束函数，剪去不满足约束条件的路径；2.使用限界函数，剪去不能得到最优解的路径。本题中，约束函数在于下面几点：

可行位置状态向量属于安全位置状态向量，可行运输状态向量属于安全运输状态向量；
历史位置状态不重复；
运输时农夫所携带个体与农夫位于同一侧。

问题的关键在于如何定义问题的解空间，转化成树（即解空间树）。解空间树分为两种：子集树和排列树。两种在算法结构和思路上大体相同。

考虑模型的搜索遍历算法，有此问题可以分解，但是又不能得出明确的递归解法，因此本文采用回溯法解决此问题。回溯法的优点在于其程序结构明确，可读性强，易于理解，而且通过对问题的分析可以大大提高运行效率。本文用采回溯法，按照深度优先搜索策略，遍历构建的位置空间状态树，输出得到的所有路径。

求解得到所有可行路径之后，根据可行路径集合中元素个数多少确定路径长短，最短路径即为所含元素最少的路径。

模型求解结果

通过回溯算法求解所建立模型，由程序语言实现（完整代码见附录）后，得到下面对模型的求解结果：

    方案1:
    [[1, 1, 1, 1], [0, 1, 0, 1], [1, 1, 0, 1], [0, 0, 0, 1], [1, 0, 1, 1], [0, 0, 1, 0], [1, 0, 1, 0], [0, 0, 0, 0]]

    方案2:
    [[1, 1, 1, 1], [0, 1, 0, 1], [1, 1, 0, 1], [0, 1, 0, 0], [1, 1, 1, 0], [0, 0, 1, 0], [1, 0, 1, 0], [0, 0, 0, 0]]

模型检验

为检验模型的正确性与普适性，现假定当狼、羊同时存在时 (农夫不存在 )，狼不会吃羊。即添加安全位置状态向量 $S_{11}=(0,1,1,0), S_{12}=(1,0,0,1)$ 。代入原模型中，利用回溯算法求解所有符合条件的农夫过河策略，得到下面的求解方案状态向量:

方案1:
[[1, 1, 1, 1], [0, 1, 0, 1], [1, 1, 0, 1], [0, 0, 0, 1], [1, 0, 0, 1], [0, 0, 0, 0]]
方案2:
[[1, 1, 1, 1], [0, 1, 0, 1], [1, 1, 0, 1], [0, 0, 0, 1], [1, 0, 1, 1], [0, 0, 1, 0], [1, 0,
1, 0], [0, 0, 0, 0]]
方案3:
[[1, 1, 1, 1], [0, 1, 0, 1], [1, 1, 0, 1], [0, 1, 0, 0], [1, 1, 1, 0], [0, 0, 1, 0], [1, 0,
1, 0], [0, 0, 0, 0]]
方案4:
[[1, 1, 1, 1], [0, 1, 0, 1], [1, 1, 0, 1], [0, 1, 0, 0], [1, 1, 1, 0], [0, 0, 1, 0], [1, 0,
1, 1], [0, 0, 0, 1], [1, 0, 0, 1], [0, 0, 0, 0]]
方案5:
[[1, 1, 1, 1], [0, 1, 1, 0], [1, 1, 1, 0], [0, 0, 1, 0], [1, 0, 1, 0], [0, 0, 0, 0]]
方案6:
[[1, 1, 1, 1], [0, 1, 1, 0], [1, 1, 1, 0], [0, 0, 1, 0], [1, 0, 1, 1], [0, 0, 0, 1], [1, 0,
0, 1], [0, 0, 0, 0]]
方案7:
[[1, 1, 1, 1], [0, 1, 1, 0], [1, 1, 1, 0], [0, 1, 0, 0], [1, 1, 0, 1], [0, 0, 0, 1], [1, 0,
0, 1], [0, 0, 0, 0]]
方案8:
[[1, 1, 1, 1], [0, 1, 1, 0], [1, 1, 1, 0], [0, 1, 0, 0], [1, 1, 0, 1], [0, 0, 0, 1], [1, 0,
1, 1], [0, 0, 1, 0], [1, 0, 1, 0], [0, 0, 0, 0]]

得到的最短路径为:

农夫带羊过河 $\rightarrow$ 农夫返回农夫 $\rightarrow$ 带狼过河 $\rightarrow$ 农夫返回 $\rightarrow$ 农夫带菜过河
农夫带羊过河 $\rightarrow$ 农夫返回 $\rightarrow$ 农夫带狼过河 $\rightarrow$ 农夫返回 $\rightarrow$ 农夫带菜过河

放宽约束要求后，所得到的合理方案数更多，最优方案所需路径更少。这与实际情况相符合。经检验，本文模型具有较高的普适性，所求方案完整准确，适用于此类约束性规划过河问题，具有较高的实际意义。

这里有点扯淡，因为我也无法说明为啥这就是只有这八种方案

模型评价

模型优点

巧妙地将问题约束条件量化，构造空间状态树的数据结构，使求解结果更加准确全面。
模型轻便，具有普适性，适于推广到不同的问题中去。
采用回溯法，DFS，提高遍历效率。在分支界限法中，一般用的是 FIFO 或最小耗费其思想是一次性将一个节点的所有子节点求出并将其放入一个待求子节点的队列。通过遍历这个队列（队列在遍历过程中不断增长）完成搜索。而 DFS 的作法则是将每一条合法路径求出后再转而向上求第二条合法路径。而在回溯法中，采用DFS。可以通过约束函数杀死一些节点从而提高算法效率，由于 DFS 是将路径逐一求出的，通过在求路径的过程中杀死节点即可省去求所有子节点所花费的时间。

模型缺点

建模方法单一，对于同一问题没有建立多个模型，无法进行多个模型的分析与比较。
模型初始化需要用户提供所有的安全位置状态集合与安全路径集合，虽简便了算法的实现，但在使用方面增加了一定的复杂程度。

参考博文

[1] https://blog.csdn.net/ltx06/article/details/24110171

[2] https://www.cnblogs.com/wj033/p/9129984.html

[3] https://www.jianshu.com/p/d28b01b3edae

[4] https://www.cnblogs.com/steven_oyj/archive/2010/05/22/1741376.html

[5] https://wenku.baidu.com/view/9005d511f18583d049645937.html