课程一： 数学思维游戏与数学悖论
提示
本课程是本人为 2021 至微公益团队暑假支教所作课程设计，教学对象分三至六年级不等，课程设计仍在不断优化中。
课程一： 数学思维游戏与数学悖论
授课背景与目的
当前教育体系下，学校的数学教育主要面向应试，而“能做题，做对题”不应该是数学教育的目标。在一昧追求数学成绩的背景下，数学成为不少孩子厌恶的学科。为了提高孩子们的数学思维与逻辑创新能力，培养孩子们对数学的兴趣，本课程让孩子们进行发现、归纳、演绎和推理训练，为高等教育的研究学习撤下种子、打下基础，从而成就了他们的创造性思维与逻辑思维。让孩子们在生活中学数学，在数学中感受生活。课程以小组内合作，小组间竞争的方式进行，以锻造孩子们的集体荣誉感，打造有效、有活力的趣味课堂。
课堂信息
人数：30人左右 助教：0-1人 课时：4课时
简要安排: 具体划分为前两节课交流数学思维游戏<一笔画><抢数与24点>，后两节课介绍简单数学悖论<悖论初步><著名数学悖论>。课程以小组内合作，小组间竞争的方式进行，授课人提供游戏题目和思路，由孩子们讨论提供游戏方案，最后由授课人总结所蕴含的数学思维逻辑。
需要物资：小奖品、（暂定：扑克牌一副、橡皮筋50条）、最好有支持PPT播放的多媒体设备。
课程规划
第一节课： 一笔画
课前介绍：
自我介绍
我们的课程是什么？数学游戏又是什么呢？
课堂规则说明：
同学们以小组为单位，5-6 人为一组，每个人都是每一组不可或缺的一份子，在本课程的进行中会有很多的抢答和比赛活动，游戏中表现好的一组会获得更高的积分，积分更高的一组将会得到奖励。
提示
重点强调：课堂中有专门的时间供大家交流，但在老师介绍游戏的时候，为了每一位同学都能明白游戏规则，每一位同学需要保持安静，在老师多次警告时，可能会扣除该小组的积分哦
游戏介绍：
“一笔画”是指笔不离开纸，而且每条线都只画一次不准重复而画成的图形。
你能用一笔画出下列图形吗？
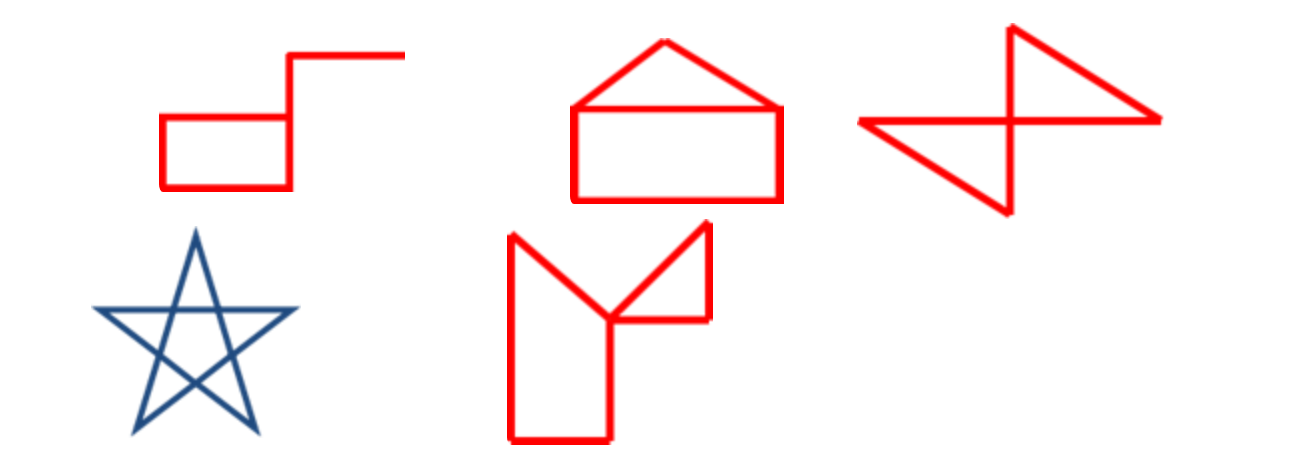那么，像汉字“日”和“中”字的图形可以一笔画成吗？“田”和“目”形呢？
游戏策略
上面的图形都可以一笔画成。“日”和“中”字形可以一笔画成，但是“田”和“目”字形不能一笔画成。这是为什么呢？
柯尼斯堡七桥问题是图论中的著名问题。这个问题是基于一个现实生活中的事例：当时东普鲁士柯尼斯堡（今日俄罗斯加里宁格勒）市区跨普列戈利亚河两岸，河中心有两个小岛。小岛与河的两岸有七条桥连接。在所有桥都只能走一遍的前提下，如何才能把这个地方所有的桥都走遍？
数学家欧拉给了我们答案，原来这与一个图形的“奇点”和“偶点”有关。我们先来了解什么是“交点”。数一数下列图形各有几个交点？
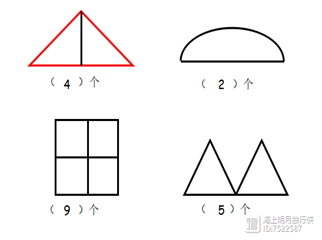
交点分为两种：
- 从这点出发的线的数目是单数的，叫单数点（奇点）。比如下面的图形就是这样的：
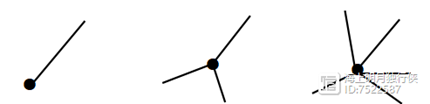
- 从这点出发的线的数目是双数的，叫双数点（偶点）。比如下面的图形就是这样的：
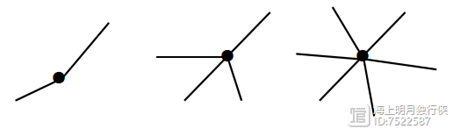
总结如下：一个图形能否一笔画成，关键在于图中双数点的多少。
（1）一笔画必须是连通的（图形的各部分之间连接在一起）；
（2）凡是图形中没有单数点的一定可以一笔画成。可选任一个点做起点，且一笔画后可以回到出发点。
（3）凡是图形中只有两个单数点，一定可以一笔画成。画时必须从一个单数点为起点，以另一单数点为终点。
（4）凡是图形中单数点的个数多于两个时，此图肯定是不能一笔画成。
下列哪些图形能一笔画出来，哪些不能？
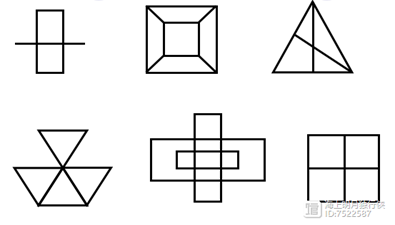
我们主要来看每个图形的“奇数点”和“偶数点”的个数。通过观察与数点，我们发现：上面一排的中间一个图形、最后一个图形和下面一排的最后一个图形的“奇数点”个数超过了两个，所以不能一笔画成。其他三个图形是可以一笔画成的。
不可以一笔画成的图形有：
（二）（三）（六）
可以一笔画成的图形有：
（一）（四）（五）
拓展思考：
想想为什么会有上面的结论呢？
练习：
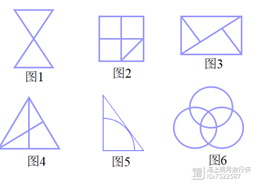
上面的图中，3、4不能一笔画成，其他都能一笔画成。
第二节课: 抢数与二十四点
抢数
游戏介绍：
两个小朋友一起做报数游戏，从1开始按数的顺序报数报道30，每人每次可以报一个数或两个数，不能不报，谁抢到30谁就赢。
在这里与小朋友们互动，让两组间的小朋友进行两两PK，并记录获胜分数
在紧张的游戏之后，授课人提出自己一定能赢，并让小朋友们与自己尝试“注意自己要是后者”，利用必胜策略，勾起小朋友的好奇。
必胜策略：
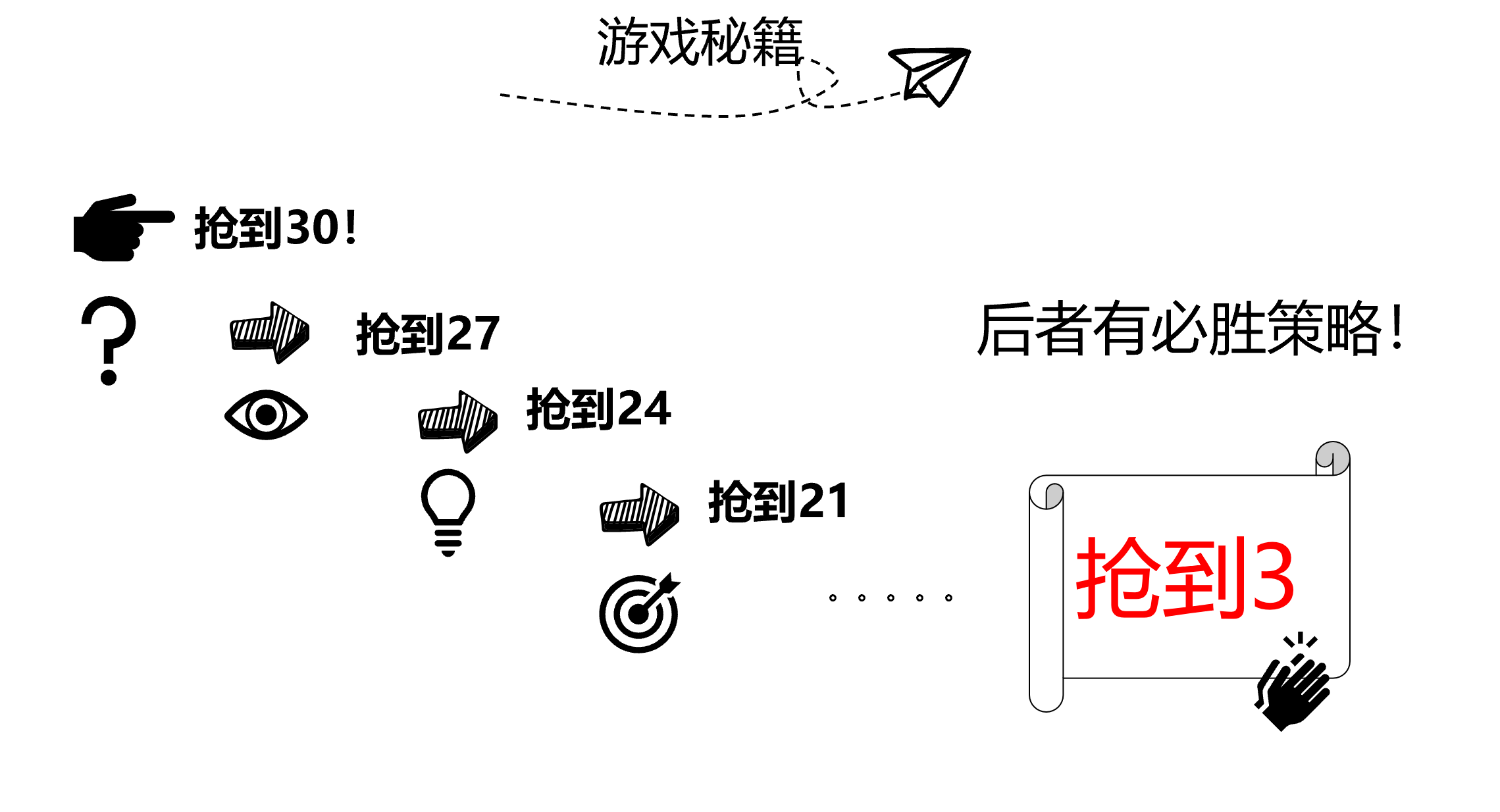
要抢到 30，必须抢到 27 ;要抢到 27，必须抢到 24 。如此倒推回去，可得到一系列关键数 30、27、24、21、18、……9、6、3。
根据以上分析，抢30游戏本身并不是一个公平的游戏，初始数和先后顺序已经决定了最后的结果，因为只有后报数者才能抢到3的倍数，后报数者有必胜策略。
拓展思考：
（1）每人每次可以报一个数或两个数，不能不报，谁抢到50谁就赢。
（2）每人每次可以报一至三个数，不能不报，谁抢到30谁就赢。
（3）每人每次可以报一至四个数，不能不报，谁抢到30谁就赢。
你学到了什么：
数学递归思想
数学是如此，人生其实也是这样，为什么我们必须要让自己比别人先迈出第一步呢？后来者居上，后发制人，看其实生活中处处有数学，数学中也处处包含着生活的道理。
二十四点
游戏介绍 ：
任意抽取一副扑克（去除J、Q、K、大王、小王）的 4 张牌，最快用加、减、乘、除（可加括号）把牌面上的数通过四则运算的方式算出 24 者胜。
举例介绍：
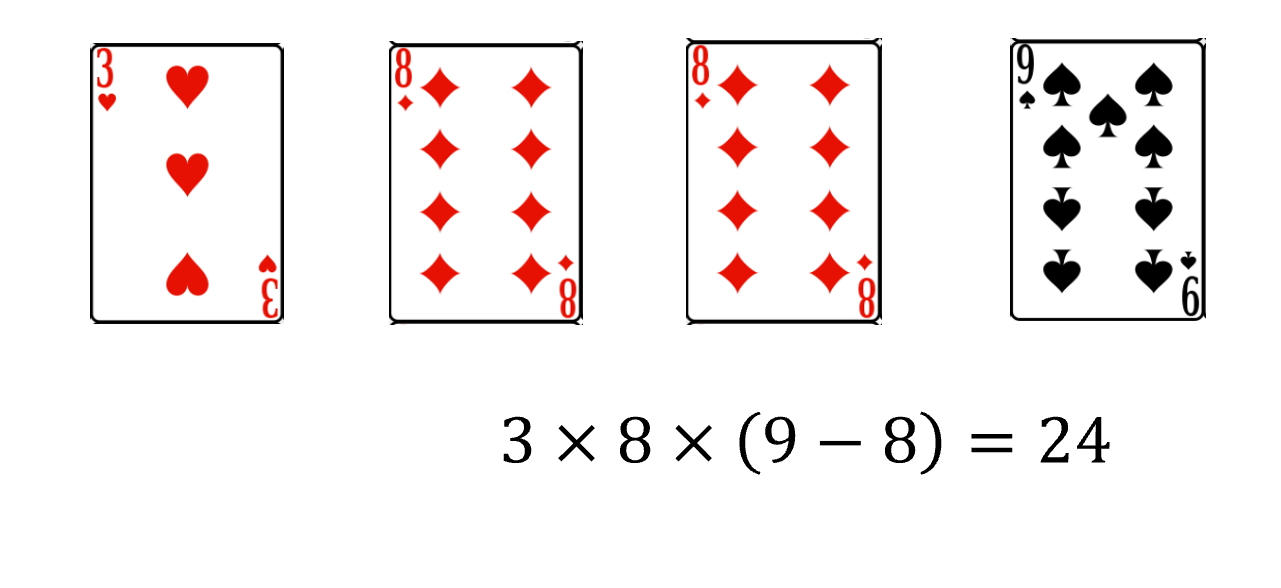
由授课人现场出题(或抽题)，让各个小组讨论协商，提供合理解者，获得得分。
给出下面的试题准备：
::: :tab 试题
1 4 9 10 6 6 2 10
6 9 3 8 9 3 1 3
4 8 1 8 8 2 1 8
3 4 5 6 3 6 6 1
4 5 1 3 2 10 2 2
2 2 4 7 2 2 10 3
7 7 1 2 5 7 2 9
:tab 答案
参考答案：
1＋4＋10＋9＝24 6＋6＋2＋10＝24
9÷（6－3）×8＝24 9×3－3×1＝24
8×4－8×1＝24 8×2＋8×1＝24
[5-（4－3）]×6＝24 6×3＋6×1＝24
4×5＋（3＋1）＝24 2×10＋2＋2＝24
（4＋7）×2＋2＝24 （10＋3）×2－2＝24
（7×7－1）÷2＝24 5×7－2－9＝24
:::
游戏策略：
- 最常见的算法是所以最先考虑的应该是上述3种算法。一般情况已有其中的一个因子，而用其他 3 个数去另一个因子。
eg: 3 2 1 4
- 消去法。3个数就可以算出24，多出来一个数，用消去法，可将多余的数除去。
eg：3 5 9 10
eg：2 5 8 8
- 上天法。先将数乘得很大，最后再除于一个数得24
eg: 10 10 4 4
- 入地法。先将数算成分数或小数，最后乘于一个数得24 eg : 3 3 7 7
极限挑战：
引出编程求解。
你学到了什么
凑配、主元、消元法
常怀对数学的热情
探索更神奇的世界
第三节课：悖论初步
小蚂蚁爬橡皮绳
问题描述：一只蚂蚁沿着一条长100米的橡皮绳以每秒1厘米的匀速由一端向另一端爬行。每过1秒钟，橡皮绳就拉长 100米，比如 10秒后，橡皮绳就伸长为1000米了。现在假定橡皮绳可任意拉长，并且拉伸是均匀的；蚂蚁也会不知疲倦地一直往前爬，在绳子均匀拉长时，蚂蚁的位置理所当然地相应均匀向前挪动。现在要问：如此下去，蚂蚁能否最终爬到橡皮绳的另一端？
让孩子们思考并让他们举手提出自己的看法，在三四个左右的回答后提出答案“小蚂蚁可以爬到橡皮绳的另一端”让孩子们理解“橡皮绳是拉伸均匀的”，可以拿一个橡皮绳画一道黑色笔记（代表蚂蚁），拉伸橡皮绳，观察黑色印记的前进方式，领会本题的要点。
悖论介绍：
上面的这种说法是正确的。但要解释清楚，却又觉得很难。这种看似这样，其实那样的数学问题（命题），数学史把它们称作“数学悖论”。什么是悖论？从数学理论的角度讲，即从一些貌似正确或看来可接受的约定出发，经过简明正确的推理，却得到自相矛盾的结论，这样的议论就称为悖论。悖论的起源几乎与数学史同步，却导致三次“数学基础危机”，使人们对数学产生怀疑，同时也从侧面促进了数学的发展。
与孩子们交流常见的悖论问题：
1、“说谎者悖论”。
这个悖论最早是在公元前六世纪出现的。当时克里特岛哲学家爱皮梅尼特曾说过：
“所有的克里特岛人都说谎”。
那么这句话是真话还是假话呢？
2、这是“说谎者悖论”的又一个变例。
让孩子们在同一张纸上写出下列两句话：
①下一句话是谎话
②上一句话是真话
这两句话该怎样理解？你能理解出来吗？
3、罗素悖论
一天，萨维尔村理发师挂出了一块招牌：村里所有不自己理发的男人都由我给他们理发。于是有人问他：“您的头发谁给理呢？”理发师顿时哑口无言。
4、上帝悖论
有个虔诚的教徒，他在演说中口口声声说上帝是无所不能的，什么事都做得到。一位过路人问了一句话：“上帝能创造一块他自己也举不起来的石头吗？”
同学们，这个虔诚的教徒能回答路人的提问吗？
5、‘不’与‘是’悖论
让孩子们进行下面的有趣的对话：
甲对乙说：“你下面要讲的是‘不’，对不对？请用‘是’或‘不’来回答！”
这句话，乙同学能回答出来吗？
第四节课：著名数学悖论
一块钱去哪了？
问题描述：
请各位小侦探们办办案，大家能否找到丢掉的一块钱呢？
有三个人去投宿,一晚三十元.三个人每人掏了10元凑够三十元交给了老板 . 后来老板说今天优惠只要25元就够了,拿出5元命令服务生退还给他们, 服务生偷偷藏起了2元, 然后,把剩下的3元钱分给了那三个人,每人分到1元.这样,一开始每人掏了10元,现在又退回1元,也就是10-1=9元，三人一共3*9=27元，加上服务员自己偷偷藏得2元一共29元，还有一元去哪里了呢？
引导孩子们思考交流其中的逻辑陷阱
个人解答：
那一元钱本身是不存在的 ，三个人住店共30元，老板退回5元，那就是说他们三人总共花了25元；然后服务员又退回每人一元，也就是说他们一共花了28元，加上老板弟弟拿的2元，刚好30元
1.总共的钱（30）=住店的人花出去的钱（27）+身上剩余的钱（3）
2.总共的钱（30）≠住店的人花出去的钱（27）+弟弟偷的钱（2）
3.住店的人花出去的钱（27）=老板赚的钱（25）+弟弟偷的钱（2）
芝诺乌龟悖论
问题描述：
阿溪里斯是古希腊神话中善跑的英雄，现在让他和乌龟赛跑。假定他的速度为乌龟的10倍。乌龟先出发，走了1米。阿溪里斯开始追赶它，当阿溪里斯走完这1米时，乌龟又向前走了0.1米；阿溪里斯再走完这0.1米时，乌龟又向前走了0.01米……阿溪里斯的速度再快，走过一段路总得花一段时间，乌龟速度再慢，在这一段时间里也总要再向前走一段路程。这样说来，阿溪里斯是永远追不上乌龟了。同学们，你认为这种说法正确吗？你能说出其中的理由吗？
从这个悖论介绍到0.9九的循环等于1这个概念
让同学们小组交流谈谈自己的看法。
结课升华：
这个问题困扰了科学家近两千多年，直到十八世纪牛顿等科学家用微积分彻底解决了这个难题，数学悖论不断推动着人类的进步。通过数学游戏，数学悖论这四节课，希望同学们能真正感受到数学的魅力，时刻保持着学习数学，解决数学难题的热情和决心，相信数学也能帮助你在今后的生活中保持缜密的思维逻辑，严谨的求实精神，真正将数学与生活联系起来，甚至帮助并推动人类数学的进步！我相信大家，我也期待你们的好消息，谢谢大家！
注意事项：
强调教课中小组间竞争与小组内合作的必要性，对较有难度的问题要有耐心、多举例的分析问题，对孩子们比较感兴趣的游戏要加以拓展。培养孩子们的数学兴趣需要及时活跃课堂气氛，但也要保证课堂纪律及课程的正常进行，将数学游戏与数学游戏中所剖析出的人生哲理要加以分析，让孩子们在游戏中学到真正受益一生的道理，拥有对数学学科的兴趣，锻炼数学思维是本课程的最高目标。
课程二：快乐乒乓
授课背景与目的
乒乓球是中国的国球，这项运动是集健身、竞技和娱乐为一体的运动，同时又是技术和战术完美结合的典型。乒乓球是一项集力量、速度、柔韧、灵敏和耐力素质为一体的球类运动，同时乒乓球具有明显的竞技性特点和娱乐功能，又使其成为一项培养机智果断等品质和保持青春活力，调节神经的有效运动。通过参加乒乓球训练可以培养人坚忍不拔的韧性，培养团队精神通过参加乒乓球训练能提高儿童少年的身体协调性、反应灵敏度，促进新陈代谢通过参加乒乓球训练可以强身健体。乒乓球运动要求全身性的协调与配合，可极大程度地改善孩子的体质，增强其心肺功能，并完善其不均衡的体型通过参加乒乓球训练可以增强体质，对保护眼睛，提高视力有很多帮助通过学习乒乓球，青少年可以扩大自己的社交范围，感受运动的激情与快乐，共同的兴趣爱好，可以结交许多朋友。打乒乓球不止是拥有一项特长，而是在打球的过程中，学会刻服，学会勤奋，学会控制情绪，学会做人！乒乓球具有安全，易上手，所需场地条件低等特点，利于小学三-六年级的小朋友培养体育兴趣爱好，增强国家自信。本课程将教授乒乓球基本规则和基本打法，致力于让每一个孩子学会基本的乒乓球玩法，培养基本的乒乓球爱好，能在今后的生活中感受乒乓球的魅力，爱上乒乓球运动。
课堂信息
人数: 30人左右 助教：1-2人 课时: 4-5课时
简要安排: 本课程将教学与学生练习相结合，通过对乒乓球具体规则的介绍开始，讲解了乒乓球基本握拍，发球，击打方法，让每一位同学会玩乒乓球。在此基础上进行旋转球、扣杀球的拓展提高，并对多人乒乓球（双打和团体）进行介绍。在每节课有充分的时间交给孩子们自主练习，学生以每四人为一组，这个过程需要授课者到每一组前去纠正孩子们的具体姿势和动作，致力于培养孩子们的运动兴趣。
需要物资: 乒乓球拍（数量为具体上课人数的一半）、乒乓球（数量为具体上课人数）、需要学校有一定数量的乒乓球桌
课程规划
第一节课：乒乓球介绍与乒乓球基本规则
室内上课，进行如下：
自我介绍和介绍对乒乓球在中国的发展：
建国后我国处于积贫积弱的状态，美国等资本主义国家封锁我国的经济，1958年以后和苏联的关系恶化，更加剧恶化了我国的国际生存空间，中国基本处于自力更生的状态。而在这个时候想要证明自己也只能从体育口取得突破，特别是1959年容国团获得世乒赛单打冠军，这是新中国的第一个世界冠军，一下子振奋人心，当时中国体育只有乒乓球一枝独秀，所以乒乓球也就是人们茶余饭后的谈资，乒乓球器材简单，所以从国家领导人到普通人都在打乒乓球，乒乓球逐渐确立了国球地位。
1961年世乒赛在北京举办，中国队取得了好成绩，男团五虎将勇夺男团冠军，团体冠军最能体现一个国家乒乓球实力。1961年1963年1965年中国连续三次获得世乒赛团体冠军，而且出现了乒乓球界的传奇人物庄则栋，因为他也连续三次获得世乒赛单打冠军，获得了圣勃莱德杯的复制杯，只有连续三次或者不连续四次才能获得世乒赛奖杯的复制杯，我印象中只有两位选手获得此殊荣：庄则栋、王楠。
中国队至此开始了长盛不衰，中间可能会有几年的低谷但都会很快重登巅峰，相对的低谷就是1989年以瓦尔德内尔佩尔森为代表的瑞典队的崛起，中国队陷入低谷，整个80年代末90年代初，中国队都在与世界强队竞争，直到1995年世乒赛中国队重夺男团冠军，中国队正式走出低谷，新一代的国乒人才出现：刘国梁孔令辉。到了王励勤马琳王皓这一批运动员中国乒乓球重登巅峰，成为世界绝对强队，变得不可战胜，2001年之后重大赛事团体赛再无失手（2010年莫斯科世乒赛女团失手），到了马龙张继科许昕三驾马车中国队已经难觅对手。
一代一代的国乒人，通过他们的努力才达到今天的成就和底蕴，今天乒乓球有完备的人才培养体系，有世界最强大的人才储备，也有世界杯强大教练队伍，当今国乒，有这样的成绩是几辈人的努力。
介绍乒乓球在中国的发展史，建立小朋友们对乒乓球的自信心：中国人擅长乒乓球
此处可以放乒乓球的精彩视频勾起小朋友的兴趣
为什么要学习乒乓球
乒乓球是一项集力量、速度、柔韧、灵敏和耐力素质为一体的球类运动，同时乒乓球具有明显的竞技性特点和娱乐功能，又使其成为一项培养机智果断等品质和保持青春活力，调节神经的有效运动。通过参加乒乓球训练可以培养人坚忍不拔的韧性，培养团队精神通过参加乒乓球训练能提高儿童少年的身体协调性、反应灵敏度，促进新陈代谢通过参加乒乓球训练可以强身健体。乒乓球运动要求全身性的协调与配合，可极大程度地改善孩子的体质，增强其心肺功能，并完善其不均衡的体型通过参加乒乓球训练可以增强体质，对保护眼睛，提高视力有很多帮助通过学习乒乓球，青少年可以扩大自己的社交范围，感受运动的激情与快乐，共同的兴趣爱好，可以结交许多朋友。打乒乓球不止是拥有一项特长，而是在打球的过程中，学会刻服，学会勤奋，学会控制情绪，学会做人！
强调说明上课纪律
以四人为一小组，第一节课在室内讲解具体规则，第二节课开始在室外学习乒乓球，具体纪律如下：
注意安全，不得擅自离开乒乓球场地，严格听从老师和助教安排。
不得损坏乒乓球拍，乒乓球和乒乓球桌，上课后先听从老师讲解具体操作，经老师同意练习后，方可散开练习。
四人一小组，轮流练习，不得与同学发生冲突与争执，有任何问题第一时间告诉老师，要主动谦让同学。
下课后主动归还乒乓球拍和乒乓球，依次回到教室，不得逗留嬉戏。
乒乓球基本规则介绍
合法发球
合法击球
常见犯规错误
第二节课：握拍、发球、基本击打、具体分析乒乓球策略
提示
根据小朋友的乒乓球基础，调整授课着重点
组织同学们有序到底体育场，并做热身运动
在这里可以与助教进行乒乓球比赛表演
教学内容：(大概15分钟左右)
一、握拍：
提供两种握拍方式供同学们选择，横排（有利于进攻）与直拍（有利于防守），建议初学者以直拍的方式击球，规范每位同学的握拍方式。
二、发球：
在乒乓球桌上，讲解乒乓球发球规则，并做演示，初学者可以采用弹发球的形式
三、基本击打：
在乒乓球桌上，讲解乒乓球击打的具体规则，要点，和具体扣分情况，并与助教进行演示（横排与直拍都演示）
练习（25分钟左右）：
每组成员四人轮流交替，授课者依次前往每一组具体指导乒乓球发球击打动作。注意关注每一位同学。对表现优异的同学要加以表扬，对暂时打的不好的同学要加以耐心的鼓励和指导。
下课（提前5分钟）：
距离下课时间提前五分钟集结队伍并点数，确保每一位同学均在队伍中，询问本节课的收获、疑惑和建议，后整齐带入教学楼中。
第三节课：反手拉杆球、正手攻球
组织同学们有序到底体育场，并做热身运动
在这里可以与助教进行乒乓球比赛表演
教学内容：（大概15分钟左右）
一、反手拉杆球：
注意讲解反手拉杆球的运用时机，具体的动作、姿势要领、反手握乒乓球拍的手势、以及乒乓球拍的角度和反手拉球的力度。
<与助教进行一对一的反手拉杆球对拉，注意强调乒乓球的运球节奏。>
二、正手攻球：
注意讲解正手攻球的运用时机，具体的动作。姿势要领、正手握乒乓球拍的手势、以及乒乓球拍的角度和正手攻球的力度。
与助教进行一对一的正手攻球对攻，注意强调乒乓球的正手攻球节奏
练习：（25分钟左右）
每组成员四人轮流交替，每两位同学进行五组反手拉杆球，五组正手攻球训练。授课者依次前往每一组，注意纠正同学们的动作和姿势和握拍。对表现优异的同学要加以表扬，对暂时打的不好的同学要加以耐心的鼓励和指导。
下课（提前5分钟）：
距离下课时间提前五分钟集结队伍并点数，确保每一位同学均在队伍中，询问本节课的收获、疑惑和建议，后整齐带入教学楼中。
第四节课：<暂定：旋转球、扣杀球/若小朋友接受较好则上这节提高课，否则跳过>
组织同学们有序到底体育场，并做热身运动
在这里可以与助教进行乒乓球比赛表演
教学内容：（大概15分钟左右）
提示
此内容为提高内容，注意因材施教
一、旋转球：
讲解旋转球的基本原理，旋转球的基本威胁方式，旋转球的基本应对方式，重点讲解旋转球的打法和旋转球的应对方法。
二、扣杀球：
讲解扣球的基本操作，重点讲解扣球的动作要领和击打力度与击打角度。讲解扣球的基本应对方式（包括防守和反攻）。
三、人生升华：
旋转球与扣球是一柔一刚，各有特点，这与中国阴阳观点相似。一昧的旋转球缺乏攻击力，一昧的扣杀球失误率高，并且防守性低，只有兼并刚柔，并内化于心，才能真正学好乒乓球，乒乓球如此，人生也是如此，这就是唯物辩证。
练习：（25分钟左右）
每组成员四人轮流交替，对不同接受程度的同学进行自主的训练，乒乓球基础较好者可以继续训练旋转球与扣杀球，或者其他同学可选择复习训练上节课内容。授课者依次前往每一组，注意纠正同学们的动作和姿势和握拍。对表现优异的同学要加以表扬，对暂时打的不好的同学要加以耐心的鼓励和指导。
下课（提前5分钟）：
距离下课时间提前五分钟集结队伍并点数，确保每一位同学均在队伍中，询问本节课的收获、疑惑和建议，后整齐带入教学楼中。
第五节课：<多人乒乓球初步>
本节课注重培养小朋友的团队协作能力与团队默契，丰富更多的乒乓球打法
组织同学们有序到底体育场，并做热身运动
在这里可以与助教进行乒乓球比赛表演
教学内容：（大概15分钟左右）
一、乒乓球双打介绍
（男子双打、女子双打、混合双打）：
中国乒乓球双打获得的荣誉
具体击打的方式与规则
注意事项
这里可以和助教选择两位同学进行双打示范
二、团体乒乓球介绍
（男子团体、女子团体）
中国团体乒乓球获得的荣誉
具体规则
练习：（25分钟左右）
每两组同学组合，先进行双打练习，注意强调乒乓球击打的顺序。
两组同学练习双打后，可进行乒乓球团体对打训练。
对表现优异的同学要加以表扬，对暂时打的不好的同学要加以耐心的鼓励和指导。
下课（提前5分钟）：
距离下课时间提前五分钟集结队伍并点数，确保每一位同学均在队伍中，询问五节乒乓球课后学生们的收获，并承诺对感兴趣的同学可以在空闲时间与自己进行乒乓球的训练和比赛，后整齐带入教学楼中。
注意事项：
室外体育课的学生安全是首位，在此前提下进行乒乓球的授课；对学生的课程教授要有耐心，并给予奖励与鼓励；在乒乓球的教学中，致力于培养孩子们运动的兴趣，并注意对孩子们民族自信、中国自信力的培养。对不同的学生要因材施教，不能以唯一标准评判每一位学生的努力。